Detect Loop in Linked List (Floyd's Cycle Detection Algorithm)

Difficulty: Medium, Asked-in: Google, Amazon, Microsoft, Goldman Sachs, Nvidia

Key takeaway: An excellent linked list problem to learn problem-solving using fast and slow pointers (Floyd's cycle detection algorithm). We can solve many other coding questions using the similar idea.

Let’s understand the problem

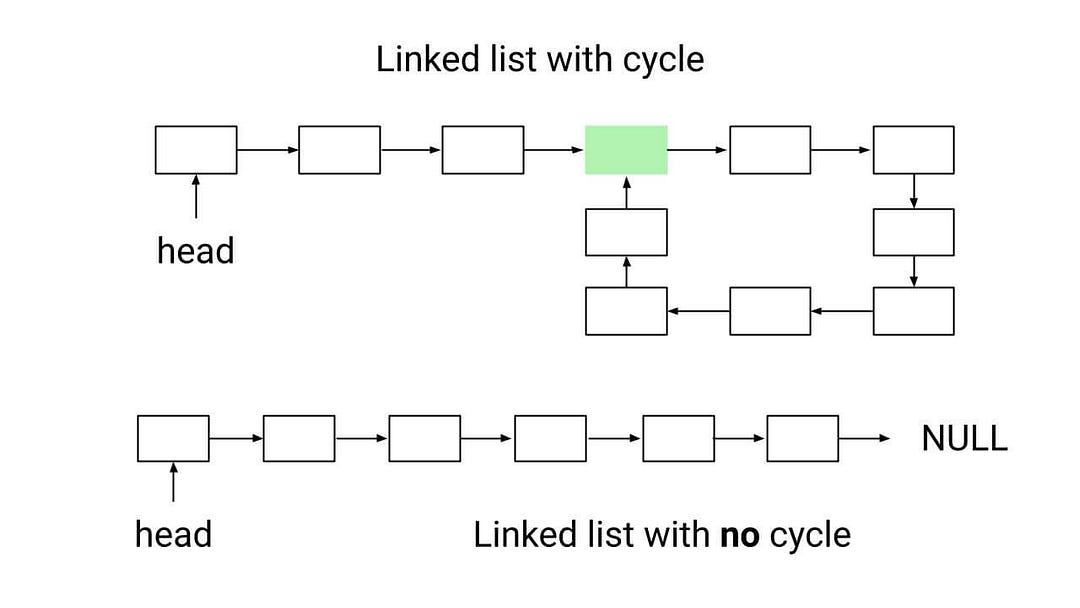
Given the head of a linked list, write a program to find if linked list has a cycle or not. Return true if there is a cycle, otherwise, return false.

Critical note related to the problem

In a singly linked list, we are usually given a reference to the first node to perform various operations such as traversal, searching, insertion, deletion, and merging. These operations require a well-formed linked list i.e. a list without loops or cycles.

To understand why, consider what happens when a linked list has a cycle. In this case, there is no "end" node and one of the nodes is the next node of two different nodes. This means that when we try to iterate through the list, we will encounter the nodes in the cycle multiple times, causing the iteration to fail. To avoid this, it is important to detect linked lists with cycles before applying an iterative approach.

Discussed solution approaches

•  Brute force approach using hash table
• Using boolean flag inside linked list node
• Efficient approach  using fast and slow pointers

 Brute force approach using hash table

Solution idea

The basic idea is to traverse the linked list and use a hash table to keep track of the nodes that have been visited during the traversal. If we encounter a node that has already been visited, it means that there is a cycle in the linked list because this node must be part of a cycle. If we reach the end of the list without encountering any visited nodes again, it means there is no cycle.

Solution code C++

bool detectLinkedListLoop(ListNode* head)
{
    unordered_map<ListNode*, bool> H;
    ListNode* currNode = head;
    while (currNode != NULL)
    {
        if (H.find(currNode) != H.end())
            return true;
        H[currNode] = true;
        currNode = currNode->next;
    }
    return false;
}

Solution code Python

def detectLinkedListLoop(head):
    H = {}
    currNode = head
    while currNode is not None:
        if currNode in H:
            return True
        H[currNode] = True
        currNode = currNode.next
    return False

Solution code Java

class Solution 
{
    public boolean detectLinkedListLoop(ListNode head) 
    {
        HashMap<ListNode, Boolean> H = new HashMap<>();
        ListNode currNode = head;
        while (currNode != null) 
        {
            if (H.containsKey(currNode))
                return true;
            H.put(currNode, true);
            currNode = currNode.next;
        }
        return false;
    }
}

Time and space complexity analysis

The above algorithm for detecting a cycle in a linked list requires only one traversal of the list. For each node, we perform one insert operation (to add the node to the hash table) and one search operation (to check if the node has been visited before). So the time complexity of this algorithm is O(n), where n is the number of nodes in the list.

This algorithm also has a space complexity of O(n) because we use a hash table to store the nodes of the linked list.

Using boolean flag inside linked list node

Solution idea

Can we optimise the above approach by avoiding the overhead of hash table operations? One way to do this is to add a "visited" flag to the structure of the linked list node. This flag can be used to mark the nodes that have been visited and detect when a node is encountered again during the traversal.

To use this optimization, we can traverse the linked list using a loop and mark the "visited" flag as 1 whenever a node is visited for the first time. If we encounter a node with the "visited" flag already set to 1, it means there is a cycle in the linked list. Note that the "visited" flag is initially set to 0 for each node.

Solution code C++

struct ListNode
{
    int data;
    ListNode* next;
    int visited;
    
    ListNode(int val)
    {
        data = val;
        next = NULL;
        visited = 0;
    }
};

bool detectLinkedListLoop(ListNode* head)
{
    ListNode* curr = head;
    while (curr != NULL)
    {
        if (curr->visited == 1)
            return true;
        curr->visited = 1;
        curr = curr->next;
    }
    return false;
}

Solution code Python

class ListNode:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.visited = 0

def detectLinkedListLoop(head):
    curr = head
    while curr is not None:
        if curr.visited == 1:
            return True
        curr.visited = 1
        curr = curr.next
    return False

Time and space complexity analysis

The above algorithm for detecting cycles in a linked list has a time complexity of O(n) because it traverses each node in the list once. However, it has a space complexity of O(n) because it uses an extra variable (the "visited" flag) for each node in the list.

Efficient solution using fast and slow pointers (Floyd's cycle detection algorithm)

Solution idea

The above solutions use O(n) space, so the critical question is: Can we optimize further and detect linked list cycle using O(n) time and O(1) space?

This idea of detecting cycles in a linked list is based on an algorithm known as Floyd's cycle finding algorithm or the tortoise and the hare algorithm. This algorithm uses two pointers, a "slow" pointer and a "fast" pointer, that move through the list at different speeds. At each iteration step, the slow pointer moves one step while the fast pointer moves two steps. If the two pointers ever meet, it means there is a cycle in the linked list. Think!

Solution steps

1. We initialize two pointers, fast" and slow, with the head node of the linked list.
2. Now we run a loop to traverse the linked list. At each step of the iteration, move the slow pointer to one position and the fast pointer to two positions.
3. If the fast pointer reaches the end of the list (i.e., fast == NULL or fast->next == NULL), there is no loop in the linked list. Otherwise, the fast and slow pointers will eventually meet at some point, indicating a loop in the linked list.

The critical question is: Why will this happen? One basic intuition is simple: If there is a loop, the fast pointer will eventually catch up to the slow pointer because it is moving at a faster pace. This is similar to two people moving at different speeds on a circular track: eventually, the faster person will catch up to the slower person.

Solution code C++

bool detectLinkedListLoop(ListNode* head)
{
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast != NULL && fast->next != NULL)
    {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast)
            return true;
    }
    return false;
}

Solution code Python

def detectLinkedListLoop(head):
    slow = head
    fast = head
    while fast is not None and fast.next is not None:
        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            return True
    return False

Some critical observations

In Floyd's cycle finding algorithm, the fast pointer moves at twice the speed of the slow pointer. This means that the gap between the two pointers increases by one after each iteration. For example, after the fifth iteration, the fast pointer will have moved 10 steps and the slow pointer will have moved 5 steps, resulting in a gap of 5.

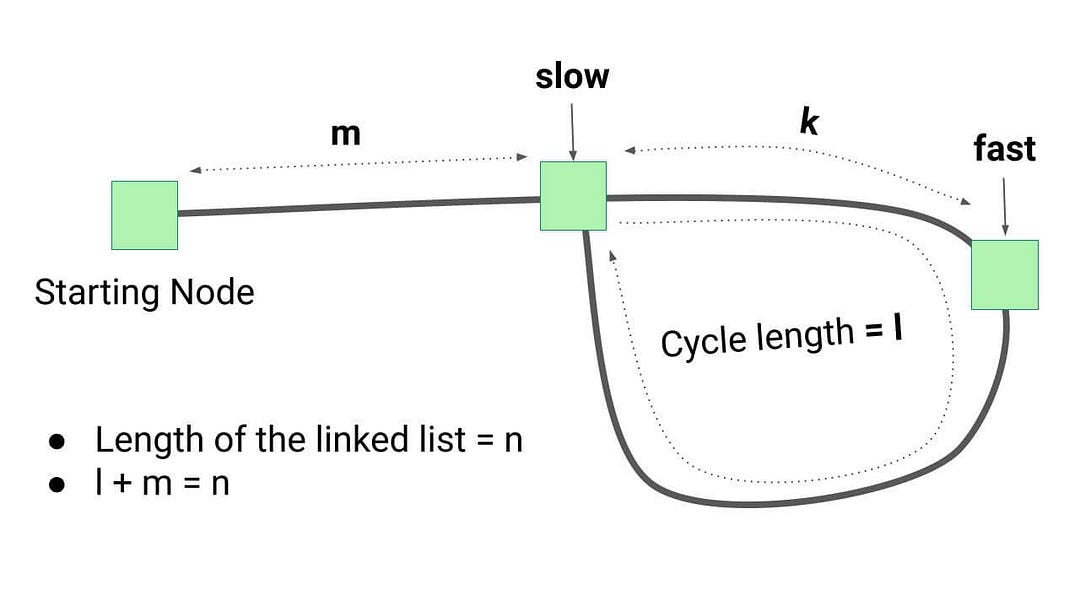
When the slow pointer enters the loop, the fast pointer is already inside the loop. Suppose at this point, the fast pointer is a distance k (k < l, where l is the length of the loop) from the slow pointer. As the two pointers move through the loop, the gap between them increases by one after each iteration. When the gap becomes equal to the length of the loop (l), the pointers will meet because they are moving in a cycle of length l. The total number of steps traveled by both pointers in the cycle before they meet at a common point is therefore l - k.

Time and space complexity analysis

Suppose:

• Total number of nodes in linked list = n
• The length of linked list cycle (if any) = l
• The distance of the cycle's starting point from beginning = m. Here l + m = n
• When slow pointer enters the loop, fast pointer distance from the slow pointer = k.

Case 1: When there is no loop in linked list.

Fast pointer will reach the end after n/2 steps. So, Time complexity = O(n).

Case 2: When there is a loop in linked list.

Both pointers will move m steps before slow pointer take entry into the loop. Inside the loop, both pointers will travel (l - k) steps before meeting at some common point. Time complexity = Total number of steps traveled by both pointers from start to meeting at common point = m + (l - k) = l + m - k = n - k (equation 1).

If slow pointer travel m distance from start to reach the bridge point, then fast pointer will travel 2m distance from the start. There will be two cases:

When m < l: k = m and total steps travelled by both pointers before meeting at a common point = n - k = n - m (From equation 1). So time complexity in the worst case = O(n), where the worst-case scenario occurs when m = 1.

When m >= l: In this situation, fast pointers will first move m distance to reach the bridge point and revolve m/l times in the cycle. So the distance of fast pointer from the bridge point (k) = m mod l 

Total no of steps travelled by both pointers before meeting at the common point = n - k = n - m mod l (From equation 1). So time complexity in the worst case = O(n), where worst-case scenario occurs when m = l.

Overall, time complexity would be O(n) in the worst case. The algorithm is working in constant space, space complexity = O(1)

Critical ideas to think!

• How do we modify the above approaches to remove the loop?
• Design an algorithm to find the loop length in the linked list.
• If there is a loop in the linked list, what would be the best-case scenario of the fast and slow pointer approach?
• How do we find the bridge node if there is any loop present?
• Can we solve this problem using some other approach?
• Is it necessary to move the fast pointer with double speed? What will happen if we move the fast pointer with speed four times the slow pointer?

Comparison of time and space complexities

•  Using hash table: Time = O(n), Space = O(n)
• Using linked list augmentation: Time = O(n), Space = O(n)
• Floyd’s cycle detection algorithm: Time = O(n), Space = O(1)

Suggested problems to practice

• Remove loop from the linked list 
• Return the node where the cycle begins in a linked list
• Swap list nodes in pairs
• Reverse a linked list in groups of a given size
• Intersection point in Y shaped linked lists

Enjoy learning, Enjoy algorithms!