Find Height or Maximum Depth of a Binary Tree
Difficulty: Medium, Asked-In: Amazon, VMWare, Zoho, Synopsys
Key takeaway: One of the fundamental tree problems to learn problem-solving using DFS (Postorder traversal) and BFS traversal.
Let’s understand the problem
Given a binary tree, write a program to find its height. In other words, we are given a binary tree and we need to calculate the maximum depth of the binary tree.
- The height or maximum depth of a binary tree is the total number of edges on the longest path from the root node to the leaf node. In other words, the height of a binary tree is equal to the maximum number of edges from the root to the most distant leaf node.
- The height of an empty tree or tree with one node is 0.
Example
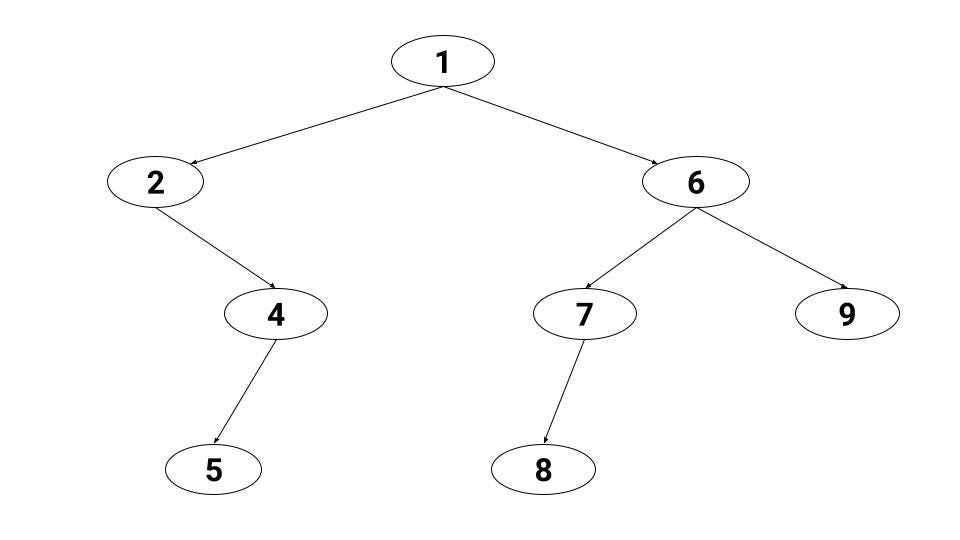
The leaf nodes of the binary tree are 5, 8, and 9.
- The number of edges from root to leaf node 5 is 3.
- The number of edges from root to leaf node 8 is 3.
- The number of edges from root to leaf node 9 is 2.
The maximum number of edges from root to farthest leaf = max(3, 3, 2) = 3. So, the height or maximum depth of the given binary tree is 3.
Discussed solution approaches
- Recursive approach: Using DFS or post-order traversal
- Iterative approach: Using BFS or level order traversal
Recursive approach: Using DFS or Post-order traversal
Solution idea
A binary tree is a recursive structure where we can solve the problem using the solution of two smaller subproblems: left sub-tree and right sub-tree. So how can we apply this idea to find the height of a binary tree? Let's think!
Based on the definition, for finding the height, we should know the path length of the root to the deepest leaf node, which can be either present in the left-subtree or right sub-tree. In other words, the longest path from the root to the deepest leaf can go through either the left or right child of the root. So the best idea would be to calculate the height of the left and right sub-tree recursively. Whichever sub-tree has the maximum height, we take that value and add 1 to get the height of the tree. Here is a clear insight:
The height of the tree = The longest path from the root node to the leaf node = 1 + max (longest path from the left-child to the leaf node, longest path from the right-child to the leaf node) = 1 + max (height of the left sub-tree, height of the right sub-tree)
So if we know the height of the left and right sub-tree then we can easily find the height of the tree. But one idea would be clear: Before calculating the height of the tree, we must know the height of the left and right sub-tree. So we need to traverse tree using post-order traversal. Think!
Solution steps
Suppose we are using the function int treeHeight(TreeNode root).
- If the tree is empty or tree has only one node, we return 0. This would be our base case.
-
Otherwise, we traverse the tree in a post-order fashion and call the same function for the left and right child to calculate the height of the left and right sub-tree.
int leftHeight = treeHeight(root->left) int rightHeight = treeHeight(root->right) -
Now after calculating the height of the left and right subtree, we take the maximum height among both and return the value by adding one to it.
if (leftHeight > rightHeight) return (leftHeight + 1) else return (rightHeight + 1)
Solution code C++
int treeHeight(TreeNode* root)
{
if (root == NULL || (root->left == NULL && root->right == NULL))
return 0;
else
{
int leftHeight = treeHeight(root->left);
int rightHeight = treeHeight(root->right);
if (leftHeight > rightHeight)
return (leftHeight + 1);
else
return (rightHeight + 1);
}
}Solution code Python
def treeHeight(root):
if root is None or (root.left is None and root.right is None):
return 0
else:
leftHeight = treeHeight(root.left)
rightHeight = treeHeight(root.right)
if leftHeight > rightHeight:
return leftHeight + 1
else:
return rightHeight + 1Solution analysis
We are doing post-order traversal for finding the height of the tree. So time complexity = O(n). Space complexity is equal to the size of the recursion call stack, which is equal to the height of the tree.
- The best-case scenario occurs when the tree is balanced, or the tree's height is O(logn). So best case space complexity = O(logn)
- The worst-case scenario occurs when the tree is highly unbalanced or skewed, i.e., there is only one node at each level. In this case, the height of the tree is O(n). So worst-case space complexity = O(n)
Explore this blog for better understanding: Recursive Tree Traversal of a Binary Tree
Iterative approach: Using BFS or Level order traversal
Solution idea
Now a critical question is: Can we find the height of the tree without recursion? Can we use level order traversal to find height? Let's think! As we know from the binary tree property => The height of the binary tree = The total number of levels in the binary tree - 1. The idea is: We traverse tree using level order traversal, count total number of levels and return the height of the tree using the above formula.
So we traverse binary tree level by level and increment a level count by 1 whenever we reach a new level. To determine the next level from the current one, we count the number of nodes at the current level, and using a loop, we add the next-level nodes to the queue until the count of nodes at the current level is 0. Then, we move on to the next level and increment the level count by 1. This process is repeated whenever we encounter a new level in the tree. At the start, the value of the level count is initialized to 0.
Explore this blog for better understanding: Level Order Traversal of a Binary Tree
Solution steps
-
We create a queue Q and push the root node into it. We also initialize a variable levelCount with 0 to track the level count of the tree.
if (root == NULL || (root->left == NULL && root->right == NULL)) return 0 int levelCount = 0 Queue Q Q.enqueue(root) -
Now we run a while loop till the Q becomes empty. In other words, this loop will explore every level. At each iteration of this loop:
- We increase levelCount by 1 and store the count of the number of nodes at the current level in a variable nodeCount (equal to the current size of the queue).
levelCount = levelCount + 1 int nodeCount = queue.size()- Now we insert children of all the nodes in the current level into the queue. For this, we run another loop till the nodeCount at the current level is 0. We check if the current node has the left and right children. If yes, we insert it into the queue.
for(int i = 0; i < nodeCount; i = i + 1) { TreeNode temp = Q.dequeue() if(temp->left != NULL) Q.enqueue(temp->left) if(temp.right != NULL) Q.enqueue(temp->right) } - If the queue is empty, it implies that the last level of the tree has been completely processed, and we return levelCount - 1 as the height of the tree.
Solution code C++
int treeHeight(TreeNode* root)
{
if (root == NULL || (root->left == NULL && root->right == NULL))
return 0;
int levelCount = 0;
queue<TreeNode*> Q;
Q.push(root);
while(!Q.empty())
{
levelCount = levelCount + 1;
int nodeCount = Q.size();
for(int i = 0; i < nodeCount; i = i + 1)
{
TreeNode* temp = Q.front();
Q.pop();
if(temp->left != NULL)
Q.push(temp->left);
if(temp->right != NULL)
Q.push(temp->right);
}
}
return levelCount - 1;
}Solution code Python
def treeHeight(root):
if root is None or (root.left is None and root.right is None):
return 0
levelCount = 0
Q = deque()
Q.append(root)
while Q:
levelCount = levelCount + 1
nodeCount = len(Q)
for i in range(nodeCount):
temp = Q.popleft()
if temp.left is not None:
Q.append(temp.left)
if temp.right is not None:
Q.append(temp.right)
return levelCount - 1Solution analysis
Time complexity = Time complexity of the level order traversal = O(n)
Space complexity = Space complexity of the level order traversal
- The worst-case space complexity = O(n), when the tree is balanced.
- The best-case space complexity = O(1), when the tree is highly un-balanced or there is only one node at each tree level.
Critical ideas to think!
- How can we solve this problem using iterative traversal using stack?
- Can we solve this problem using pre-order or in-order traversal?
- Can we think of implementing the BFS approach using some other technique? Can we use a NULL value to identify the new level in the tree?
Similar coding questions to practice
- Find min depth of a binary tree
- Merge two binary tree
- Count half nodes in a Binary tree
- Count full nodes in a Binary tree
- Deepest right leaf node in a binary tree
- Get the level of a node in a binary tree
- Check if two trees are identical
- Print all nodes at distance K from a given node
Enjoy learning! Enjoy algorithms!
