Find Next Greater Element

Difficulty: Medium, Asked-in: Amazon, Microsoft

Key takeaway: An excellent problem to learn problem-solving using a stack.

Let’s understand the problem

Given an array, find the Next Greater Element for every element. The Next Greater Element for an element is the first greater element on the right side of the array. Elements for which no greater element exist, consider the next greater element as -1.

Examples

Input: A[] = [3, 2, 8, 7, 9, 17, 12], Output: [8, 8, 9, 9, 17, -1, -1]

Explanation: Traversing through the array for each element, we find the next greater element on its right side, i.e., NGE of 3 is 8, NGE of 2 is 8, NGE of 8 is 9, NGE of 7 is 9, and so on.

Input: A[] = [4, 5, 2, 25, 10], Output: [5, 25, 25, -1, -1]

Discussed solution approaches

Brute force approach using nested loops
Efficient solution using stack : Traversing from left to right
Efficient solution using stack : Traversing from right to left

Brute force using nested loops

Solution idea and steps

The basic idea would be to traverse the array and find the next greater element for each element on the right side. We can simply use two nested loops for this.

We run an outer loop from i = 0 to n-1 to access each element X[i] in the array and run an inner loop from j = i + 1 to n-1 to access all other elements on the right side of the current element X[i]. Inside the inner loop, we find the next greater element of the element X[i].
We use an extra array output[n] to store the next greater element for each element. When we find the next greater element for an element, we break from the inner loop and store it at output[i].
Otherwise, the inner loop will go till the end, and we won't find an element that is greater than the element X[i]. In this situation, we store -1 at output[i].
By the end of the loop, we return the array output.

Solution code C++

int* nextGreaterElement(int X[], int n) 
{ 
    int nextGreater;
    int* output = new int[n];
    for (int i = 0; i < n; i  = i + 1) 
    { 
        nextGreater = -1;
        for (int j = i + 1; j < n; j = j + 1) 
        { 
            if (X[i] < X[j]) 
            { 
                nextGreater = X[j];
                break;
            } 
        } 
        output[i] = nextGreater;  
    } 
    return output;    
}

Solution code Python

def nextGreaterElement(X, n):
    output = [0] * n
    for i in range(n):
        nextGreater = -1
        for j in range(i+1, n):
            if X[i] < X[j]:
                nextGreater = X[j]
                break
        output[i] = nextGreater
    return output

Time and space complexity analysis

Here, the outer loop runs n times, and for each iteration of the outer loop, the inner loop runs n-i-1 times. So the total number of loop iterations = n - 1 + n - 2 + .... + 1 + 1 = n(n-1)/2 + 1 = O(n^2). We are performing an O(1) operation at each loop iteration, so the time complexity = O(1) * O(n^2) = O(n^2).

The space complexity is O(n) because we are using an extra output[] array of size n to store the next greater element for each element.

Efficient solution using stack: Traversing from left to right

Solution idea

Now the critical question is: how do we improve the time complexity? Is there some pattern in the problem that could help us find an efficient solution? Let's think!

Next greater elements in an array visualisation

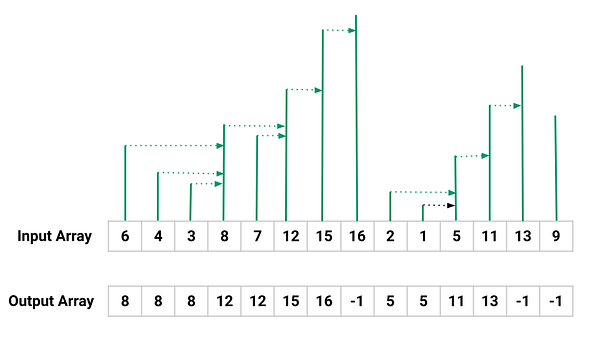
If we look at the input array from left to right, then there are two observations:

Case 1 (Decreasing order sequence): In this case, the first next greater value is the next greater element of all the values in the decreasing sequence. For example, 6, 4, and 3 are in decreasing order, so the next greater element would be 8 which is the first next greater value. Similarly, 8, 7, and 2, 1 are in decreasing order, so their next greater element would be 12 and 5.

Case 2 (Increasing order sequence): In this case, all the next values are greater than their previous value, so the adjacent element of each element is the next greater element. For example, 12, 15, and 16 are in increasing order, so the next greater element of 12 would be 15, and the next greater element of 15 would be 16. Similarly, 5, 11, and 13 are in increasing order, so the next greater element of 5 would be 11, and the next greater element of 11 would be 13.

So one idea is to scan from left to right, and when we find the first element that is greater than the previous element, we stop and save it as the next greater element of the previous element. Even this greater element can be the next greater element of some previous consecutive elements.

The critical question is: how do we identify such previous elements? The idea is simple: we need a mechanism to store the occurrences of the previous elements, i.e., we can use the stack for this purpose!

Solution steps

We create an empty stack called s.
We also declare an array called output[n] to store the next greater elements.
Now we traverse the array from left to right and push each element into the stack until the element at the top of the stack is greater than the current element.
Once the current element is greater than the top element in the stack, we keep popping elements in a loop until the top of the stack is smaller than the current element or the stack becomes empty. During this process, we set the current element as the next greater element of all the popped elements.
Now we push the current element into the stack and repeat the above process.
Once all the elements in the array are processed, the stack may not be empty. So remaining elements in the stack do not encounter any greatest element. Therefore, we pop the elements from the stack and update their next greater element to be -1.
By the end of the above process, we return the output[] array.

Note: We are pushing indices into the stack instead of the actual elements.

Solution code C++

vector<int> nextGreaterElement(int X[], int n) 
{ 
    stack<int> s;
    vector<int> output(n);
    s.push(0);
    for (int i = 1; i < n; i = i + 1) 
    {      
        while (!s.empty() && X[s.top()] <= X[i]) 
        {          
            output[s.top()] = X[i];
            s.pop();
        }
        s.push(i);
    } 
    while (!s.empty()) 
    { 
        output[s.top()] = -1;
        s.pop();
    }
    return output;    
}

Solution code Python

def nextGreaterElement(X, n):
    s = []
    output = [0] * n
    s.append(0)
    for i in range(1, n):
        while s and X[s[-1]] <= X[i]:
            output[s[-1]] = X[i]
            s.pop()
        s.append(i)
    while s:
        output[s[-1]] = -1
        s.pop()
    return output

Time and space complexity analysis

Every element is pushed and popped at most once from the stack. So the time complexity is O(n). In the worst-case scenario, the space complexity is O(n) for the stack.

Efficient solution using stack: Traversing from right to left

Solution idea

The idea is similar to the previous approach, but we process elements from right to left in the array.

We create an empty stack s.
We also declare an output[n] array to store the next greater element.
Now we run a loop from i = n - 1 to 0 to access each array element to find the next greater element.
- We push elements into the stack when the stack is empty or s.top() > X[i]. In other words, the stack will maintain the order of elements in decreasing order.
- When we find s.top() <= X[i] and the stack is not empty, we continuously pop elements from the stack.
- After the above process ends, if the stack is not empty, then the next greater element of X[i] will be present at the top of the stack, and we update it with the value s.top().
- If the stack is empty, we update -1 as the next greater element of X[i].
By the end of the above process, we return the output[n] array.

Note: Here, we are pushing actual elements into the stack.

Solution code C++

vector<int> nextGreaterElement(int X[], int n) 
{ 
    stack<int> s;
    vector<int> output(n);
    s.push(0);
    for (int i = n - 1; i >= 0; i = i - 1) 
    {
        while (!s.empty() && s.top() <= X[i])
            s.pop();
        if(!s.empty())
            output[i] = s.top();
        else 
            output[i] = -1;
        s.push(X[i]);
    }
    return output;   
}

Solution code Python

def nextGreaterElement(X, n):
    s = []
    output = [0] * n
    s.append(0)
    for i in range(n - 1, -1, -1):
        while s and s[-1] <= X[i]:
            s.pop()
        if s:
            output[i] = s[-1]
        else:
            output[i] = -1
        s.append(X[i])
    return output

Time and space complexity analysis

Every element is pushed and popped at most once to the stack. So time complexity = O(n). Space complexity in the worst case = O(n), for the stack.

Critical ideas to think!

Can we solve this problem using some other approaches?
Can we try to use other data structures other than the stack? If yes, then which one?
What will be the worst and best-case scenario of the space complexity in the stack-based approaches?
How do we modify the above approaches if the given array is circular?

Comparison of time and space complexities

Using nested loops: Time = O(n^2), Space = O(1)
Stack solution traversing from left to right: Time = O(n), Space = O(n)
Stack solution traversing from right to left: Time = O(n), Space = O(n)

Find Next Greater Element for Every Element in an Array

Let’s understand the problem

Examples

Discussed solution approaches

Brute force using nested loops

Solution idea and steps

Solution code C++

Solution code Python

Time and space complexity analysis

Efficient solution using stack: Traversing from left to right

Solution idea

Solution steps

Solution code C++

Solution code Python

Time and space complexity analysis

Efficient solution using stack: Traversing from right to left

Solution idea

Solution code C++

Solution code Python

Time and space complexity analysis

Critical ideas to think!

Comparison of time and space complexities

Suggested coding questions to practice

More from EnjoyAlgorithms

Self-paced Courses and Blogs