Introduction to Hashing and Hash Table in Data Structure

Why do we need hash table?

Many applications, such as compilers that translate programming languages, require an efficient mechanism to support dictionary operations like insert, search, and delete. For instance, a compiler may maintain a symbol table where the keys of elements are character strings corresponding to identifiers in the language. In order to support the various operations needed by the compiler, the symbol table needs to be efficient.

One issue with using arrays or linked lists to implement symbol table or dictionary operations is the time required to search for an element. For example, if the data is stored in an array, the time required to search for an element will be either O(log n) or O(n), depending on whether the array is sorted or not. In cases where we need to process a large dataset, the O(n) scenario may not be a viable option due to the time required for the search.

On the other hand, searching for an element in a hash table typically takes O(1) time on average, with a worst-case time of O(n). While it is possible for hashing to take O(n) time in the worst case, it generally performs exceptionally well on average. Therefore, it is important to understand the concept of hashing and related concepts such as hash tables and hash functions.

Direct Address Table

If an application requires a data storage mechanism where each element has a small key and the keys are distinct integers from 0 to m - 1, we can use an array T[0..m-1] to store the elements. The element with key k is placed at T[k], and T[i] is set to NIL if there is no element with key i. Depending on the application, we can either store the value itself at T[k] or just a pointer to the value.

This approach allows us to easily access the elements using their keys, as we can look up the element at the corresponding index in the array. In other words, the idea of a direct address table allows dictionary operations like insert, search, and delete to be performed in O(1) time. However, it may not be the most efficient solution if the range of keys is large. Think!

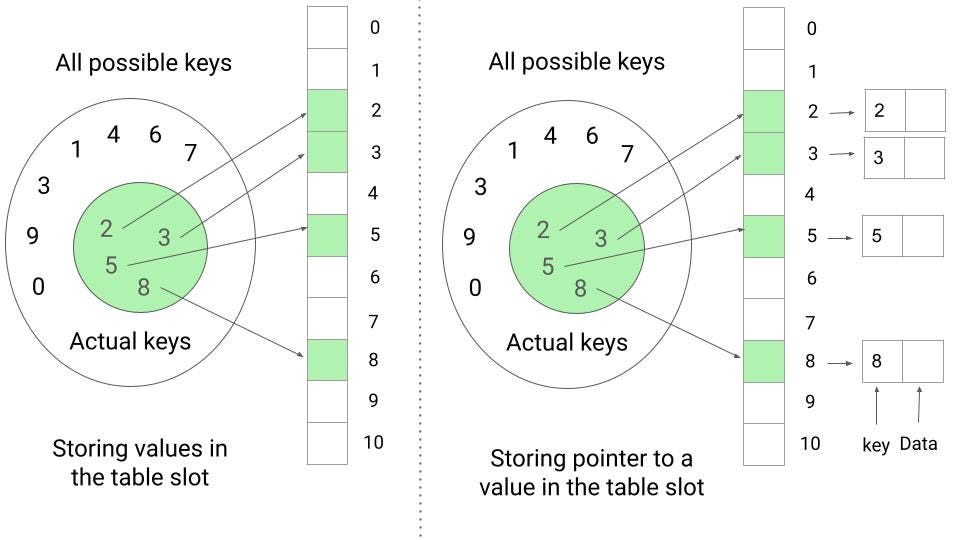
In the example shown in the image, the universe of all possible keys {0, 1, 2,....9} corresponds to the indices in the table. The set of actual keys {2, 3, 5, 8} determines which slots in the table store values or pointers to values. For example, to insert an element with key 5, we can place it at T[5]. To search for an element with key 3, we can look up T[3] in the table. To delete an element with key 8, we can set T[8] to NIL. All of these operations take O(1) time.

Challenges with Direct Address Table

There are a few key points to consider when using a direct address table:

• It is necessary to have an idea of the upper limit of keys in advance.
• The direct address table is most effective when the keys are in a small range.
• If the actual number of keys is small compared to the total number of possible keys, the direct address table can lead to a waste of memory space. This is because the table requires an array with one slot for every possible key.

In summary, the direct address table is a useful data structure when the keys are integers in a small range and we can afford to allocate an array with one slot for every possible key. If the keys are not integers or the range is large, we need an efficient data structure to perform dictionary operations.

How does Hash Table work?

A hash table is a data structure that allows efficient storage and retrieval of elements using keys of any data type. It is a good alternative to a direct address table when the actual number of keys is small compared to the total number of possible keys.

To use a hash table, we first define a hash function h(k) that calculates the array index, or "slot," from the key k. The element with key k is then stored at this slot in the hash table. The hash function enables the hash table to store and access elements using keys of any data type rather than being limited to integer keys in a small range.

The hash table requires much less storage than a direct address table, as it uses an array of size proportional to the number of actual keys rather than one slot for every possible key. This allows us to reduce the storage requirement to O(m) (where m is the total number of actual keys) while still maintaining the benefit of O(1) average search time.

Hashing involves three main steps:

1. Preprocessing the input data to calculate a key (an integer). The key does not have to be an integer itself, but can be derived from relevant information in the input data.
2. Using a hash function to transform the key into an array index.
3. Using the index generated by hash function to insert, delete, or access the desired value in the hash table.

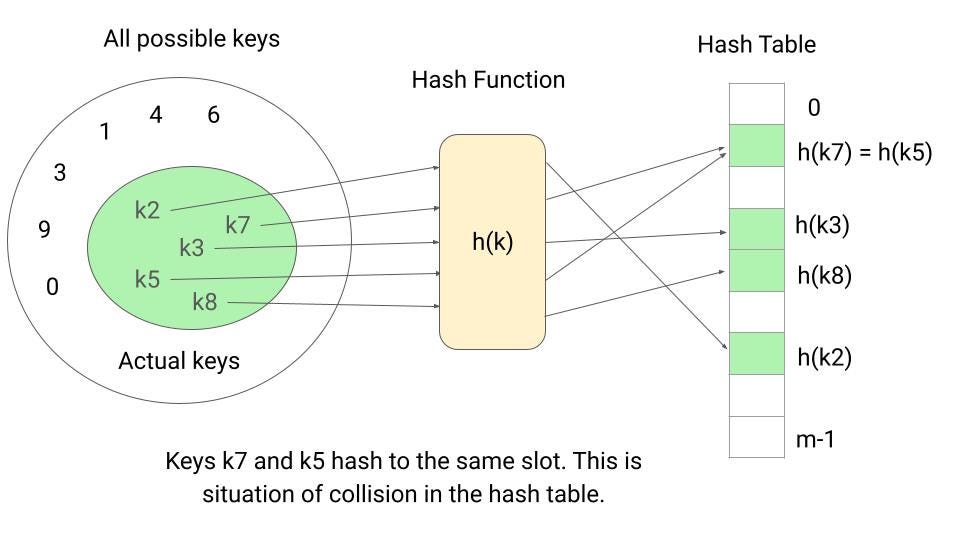
The problem of collision in the Hash Table

One potential issue with hashing is that two keys can be hashed to the same slot, known as a collision. While it is ideal to avoid collisions altogether, this is not practically possible. Therefore, it is necessary to have a plan for resolving collisions when they occur.

One way to minimize the number of collisions is to choose a well-designed, "random-looking" hash function. However, even with a good hash function, collisions can still occur. In such cases, we need a method for resolving the collisions. There are two main approaches to collision resolution: chaining and open addressing.

In chaining, elements with colliding keys are stored in a linked list at the same slot in the hash table. In open addressing, the hash table uses a probing sequence to search for an empty slot to store the colliding element. We will discuss these approaches in more detail in a separate blog post.

Explore hash function blog to understand the ideas and properties of several hash functions. 

Hashing is a time-memory tradeoff!

Hashing is a technique that allows us to balance the trade-off between time and memory when searching for elements using keys. In an ideal situation without memory limitations, we could search for an element using only one memory access by simply using the key as an index in a large array. However, this is not practical when the total number of possible keys is much larger than the actual number of keys, as it would require excessive memory.

On the other hand, we could use a linear search in an unordered array if there are no time limitations, but this would be inefficient when the number of elements becomes large.

Hashing provides a way to balance these two extremes by allowing us to adjust parameters to trade-offs between time and memory. This is achieved without rewriting code, making it a flexible and efficient technique for searching for elements using keys.

What do you mean by a good hash function?

In hashing, a good hash function is essential for efficiently storing and retrieving elements using keys. A good hash function should be easy to compute in O(1) time and uniformly distribute keys in the hash table. This is known as the assumption of uniform hashing, which states that each key is equally likely to hash to any of the m slots in the hash table.

However, it is not possible for any hash function to completely avoid collisions, so we need to have strategies in place for handling them. In future blog posts, we will discuss techniques for resolving collisions, implementing hash table operations, and problem-solving using hashing.

Overall, a good hash function and effective collision resolution strategies are crucial for effectively using a hash table to store and retrieve elements using keys.

References

• Book: Algorithms by CLRS
• Book: Algorithms by Robert Sedgewick
• Book: Algorithm design manual by Steven Skiena