Longest Common Subsequence
Difficulty: Medium, Asked-in: Google, Amazon, Uber, Hike
Key Takeaway: This is an excellent problem to learn problem solving using dynamic programming and space complexity optimization. We can solve many other DP questions using this idea.
Let’s Understand the Problem!
You are given two character strings X and Y of size m and n (m >= n). Write a program to find the length of the longest common subsequence (LCS). In other words, we need to find the length of the longest subsequence that appears in both X and Y.
- A subsequence is a new string created by deleting some characters (or none) from the original string but keeping the relative order of the remaining characters unchanged. For example, ACE, BD, ACDE, etc., are subsequences of the string ABCDE. On the other hand, a common subsequence is a subsequence that appears in both X and Y.
- If there is no common subsequence between X and Y, the program should return 0.
- It's important to note that there may be multiple common subsequences of the longest length, but we only need to return the length of the longest one.
Example 1
Input: X = [A, B, C, B, D, A, B], Y = [B, D, C, A, B, A], Output: 4
Explanation: There are many common subsequences of X and Y. For example, the sequence [B, C, A] is a common subsequence but it is not the longest one. If we observe closely, the subsequences [B, C, B, A] and [B, D, A, B] are the longest common sequences present in both strings. So X and Y have the longest common subsequence of length 4.
Example 2
Input: X = [E, B, T, B, C, A, D, F], Y = [A, B, B, C, D, G, F], Output: 5
Explanation: The longest common subsequence is [B, B, C, D, F].
Discussed solution approaches
- Brute force approach using recursion
- Using top-down approach of dynamic programming
- Using bottom-up approach of dynamic programming
- Space-optimized version of the bottom-up approach
- Efficient space-optimized version of the bottom-up approach
Brute force approach using recursion
Solution idea
This is an optimization problem where the solution space is huge, i.e., there can be so many common subsequences of both strings, and we need to find a common subsequence with the longest length. One idea would be to explore all the subsequences of both strings and find the longest among them.
When we need to explore all possibilities, we can use the idea of recursion. The critical question would be: How do we explore all the subsequences recursively? Let's think!
Here we have one obvious choice at the start: Do the last characters of both strings equal? If both are equal, that common character will be part of the longest subsequences. Let's assume the function lcs(X, Y, m, n) returns the length of the longest common subsequence.
Case 1: If the last characters of strings are equal, i.e., if(X[m - 1] == Y[n - 1]), then the problem gets reduced to finding the longest common subsequence of the remaining substrings of input size m - 1 and n - 1. So we recursively call the same function with input size (m - 1, n - 1) and add 1 to get the output for input size (m, n), i.e., lcs(X, Y, m, n) = 1 + lcs(X, Y, m - 1, n - 1).

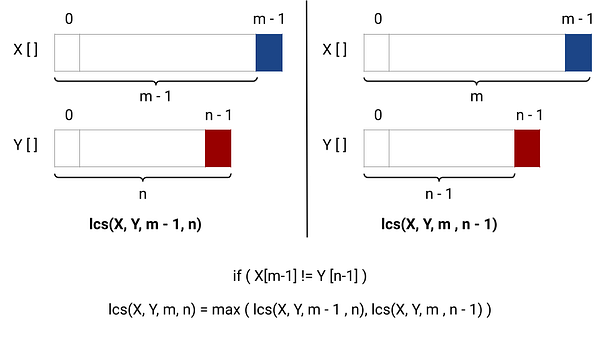
Case 2: If the last characters of the strings are not equal, i.e., if (X[m - 1] != Y[n - 1]), there are two possibilities for smaller sub-problems, and we need to find the maximum of them.
- Find the length of the longest common subsequence by excluding the last character of string X and including the last character of string Y, i.e., lcs(X, Y, m - 1, n).
- Find the length of the longest common subsequence by including the last character of string X and excluding the last character of string Y, i.e., lcs(X, Y, m, n - 1).
Either of these possibilities can provide the length of the longest common subsequence. So, we need to take the maximum of both possibilities, i.e., lcs(X, Y, m, n) = max ( lcs(X, Y, m - 1, n), lcs(X, Y, m, n - 1) ).
Base case: Recursion will terminate when any one of the string sizes gets reduced to 0 i.e. if (m == 0 || n == 0), return 0.
Solution code C++
int lcs(string X[], string Y[], int m, int n)
{
if (m == 0 || n == 0)
return 0;
if (X[m - 1] == Y[n - 1])
return 1 + lcs(X, Y, m - 1, n - 1);
else
return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n));
}Solution code Python
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0
if X[m - 1] == Y[n - 1]:
return 1 + lcs(X, Y, m - 1, n - 1)
else:
return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n))Time and space complexity analysis
There are two choices for each character in a string: it can either be included in the subsequence or not. This means there are 2^m possible subsequences of X and 2^n possible subsequences of Y. So in this recursive approach, we are comparing each subsequence of X with each subsequence of Y. So the overall time complexity is O(2^m * 2^n) = O(2^(m + n)), which is inefficient for large values of m and n.
The space complexity of this solution depends on the size of the call stack, which is equal to the height of the recursion tree. In this case, input parameters (m and n) are at most decreasing by 1 on each recursive call and terminate when either m or n becomes 0. The height of the recursion tree in the worst case will be O(max(m, n) and space complexity = O(max(m, n)).
Here time complexity is exponential because there are overlapping sub-problems, i.e., same sub-problems are repeatedly solved during recursion. This can be visualized better by drawing a recursion tree diagram. For example, in the following diagram of the recursion tree, the subproblem of size (m - 1, n - 1) comes twice. We can observe other repeating subproblems if we expand the recursion tree further.
Using top-down approach of dynamic programming
Solution idea
The problem with the recursive solution is that the same subproblems get solved many times. Each subproblem consists of two parameters, which are at most decreasing by 1 during each recursive call. So, there are (m + 1) * (n + 1) possible subproblems, and some of these subproblems get solved again and again.
Therefore, an efficient approach would be to use the top-down approach of dynamic programming (memoization) and store the solution to each subproblem in an extra memory or lookup table. When we encounter the same subproblem again during recursion, we can look into the extra memory and return the already calculated solution directly, instead of computing it again.
This could help us reduce a lot of computation and significantly improve the time complexity.
- To implement the memoization approach, we can take extra memory of size equal to the total number of different subproblems, i.e., (m + 1) * (n + 1), where we store the subproblem of input size (i, j) at the index [i + 1][j + 1] (0 <= i <= m and 0 <= j <= n).
- In the longest common subsequence, no result is negative, so we can use -1 as a flag to initialize each table entry and tell the algorithm that nothing has been stored yet.
Solution pseudocode
int lcsLength(string X[], string Y[], int m, int n)
{
int LCS[m + 1][n + 1]
for(int i = 0; i <= m; i = i + 1)
{
for (j = 0; j <= n; j = j + 1)
{
LCS[i][j] = -1
}
}
return lcs(X, Y, m, n, LCS)
}
int lcs(string X[], string Y[], int m, int n, int LCS[][])
{
if (m == 0 || n == 0)
return 0
if (LCS[m][n] < 0)
{
if (X[m - 1] == Y[n - 1])
LCS[m][n] = 1 + lcs(X, Y, m - 1, n - 1, LCS)
else
LCS[m][n] = max (lcs(X, Y, m, n - 1, LCS), lcs(X, Y, m - 1, n, LCS))
}
return LCS[m][n]
}Solution code C++
int lcs(string X[], string Y[], int m, int n, vector<vector<int>> &LCS)
{
if (m == 0 || n == 0)
return 0;
if (LCS[m][n] < 0)
{
if (X[m - 1] == Y[n - 1])
LCS[m][n] = 1 + lcs(X, Y, m - 1, n - 1, LCS);
else
LCS[m][n] = max(lcs(X, Y, m, n - 1, LCS), lcs(X, Y, m - 1, n, LCS));
}
return LCS[m][n];
}
int longestCommonSubsequence(string X[], string Y[], int m, int n)
{
vector<vector<int>> LCS(m + 1, vector<int>(n + 1, -1));
return lcs(X, Y, m, n, LCS);
}Solution code Python
def lcs(X, Y, m, n, LCS):
if m == 0 or n == 0:
return 0
if LCS[m][n] < 0:
if X[m - 1] == Y[n - 1]:
LCS[m][n] = 1 + lcs(X, Y, m - 1, n - 1, LCS)
else:
LCS[m][n] = max(lcs(X, Y, m, n - 1, LCS), lcs(X, Y, m - 1, n, LCS))
return LCS[m][n]
def longestCommonSubsequence(X, Y, m, n):
LCS = [[-1] * (n + 1) for _ in range(m + 1)]
return lcs(X, Y, m, n, LCS)Time and space complexity analysis
In the worst case, we will be solving each subproblem only once, and there are (m + 1) x (n + 1) different subproblems. So, the time complexity is O(mn). We are using a 2D table of size (m + 1) x (n + 1) to store the solutions of the subproblems. So the space complexity is O(mn).
The time complexity might be better if not all array entries get filled out. For example, if two strings match exactly, we only fill in diagonal entries, and the algorithm will be fast. Think!
Using bottom-up approach of dynamic programming
Solution idea and steps
This is a dynamic programming problem, so we can solve it efficiently using the bottom-up approach. Here, our aim is to calculate the solution to smaller problems in an iterative way and store their result in a table. The critical question is: How do we build the solution in a bottom-up manner? Here are the steps:
- Table structure: The state of smaller subproblems depends on input parameters m and n because at least one of them decreases after each recursive call. So we need to construct a 2D table LCS[][] to store the solution of the subproblems.
- Table size: The size of the 2D table will be equal to the number of different subproblems, which is (m + 1) x (n + 1).
- Table initialization: Before building the solution using the iterative structure, we need to initialize the table by the smaller version of the solution, i.e., the base case. Here, m = 0 and n = 0 are the situations of the base case, so we initialize the first row and the first column of the table with 0.
-
Iterative structure to fill the table: Now, we need to define an iterative structure to fill the table LCS[][] i.e., a relation by which we build the solution of the larger problem using the solution of smaller subproblems in a bottom-up manner. We can easily define an iterative structure by using the recursive structure of the recursive solution.
- LCS[i][j] = 1 + LCS[i - 1][j - 1], if (X[i - 1] == Y[j - 1]).
- LCS[i][j] = max(LCS[i][j - 1], LCS[i - 1][j]), if (X[i - 1] != Y[j - 1]).
- Returning the final solution: After filling the table iteratively, our final solution gets stored at the bottom left corner of the 2D table, i.e., return LCS[m][n] as an output.
Solution code C++
int lcs(string X[], string Y[], int m, int n)
{
int LCS[m + 1][n + 1];
for (int i = 0; i <= m; i = i + 1)
LCS[i][0] = 0;
for (int j = 0; j <= n; j = j + 1)
LCS[0][j] = 0;
for (int i = 1; i <= m; i = i + 1)
{
for (int j = 1; j <= n; j = j + 1)
{
if (X[i - 1] == Y[j - 1])
LCS[i][j] = 1 + LCS[i - 1][j - 1];
else
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1]);
}
}
return LCS[m][n];
}Solution code Python
def lcs(X, Y, m, n):
LCS = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if X[i - 1] == Y[j - 1]:
LCS[i][j] = 1 + LCS[i - 1][j - 1]
else:
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])
return LCS[m][n]Time and space complexity analysis
Time complexity = Time complexity of initializing the table + Time complexity of filling the table in a bottom-up manner = O(m + n) + O(mn) = O(mn). Space complexity = O(mn) for storing the table size (m + 1)*(n + 1).
Space-optimized solution of bottom-up approach
If we observe the previous 2D solution, we are only using adjacent indexes in the table to build the solution in a bottom-up manner. In other words, we are using LCS[i - 1][j - 1], LCS[i][j - 1], and LCS[i - 1][j] to fill the position LCS[i][j]. So there are two basic observations:
- We are filling entries of the table in a row-wise fashion.
- To fill the current row, we only need the value stored in the previous row.
So there is no need to store all rows in the LCS[][] matrix, and we can just store two rows at a time. In other words, we can use a two-row 2D array LCS[2][n + 1] to store values and get the output.
Solution code C++
int lcs(string X[], string Y[], int m, int n)
{
int LCS[2][n + 1];
for (int i = 0; i <= 1; i = i + 1)
LCS[i][0] = 0;
for (int j = 0; j <= n; j = j + 1)
LCS[0][j] = 0;
for (int i = 1; i <= m; i = i + 1)
{
for (int j = 1; j <= n; j = j + 1)
{
if (X[i - 1] == Y[j - 1])
LCS[i % 2][j] = 1 + LCS[(i - 1) % 2][j - 1];
else
LCS[i % 2][j] = max(LCS[(i - 1) % 2][j], LCS[i % 2][j - 1]);
}
}
return LCS[m % 2][n];
}Solution code Python
def lcs(X, Y, m, n):
LCS = [[0] * (n + 1) for _ in range(2)]
for i in range(2):
LCS[i][0] = 0
for j in range(n + 1):
LCS[0][j] = 0
for i in range(1, m + 1):
for j in range(1, n + 1):
if X[i - 1] == Y[j - 1]:
LCS[i % 2][j] = 1 + LCS[(i - 1) % 2][j - 1]
else:
LCS[i % 2][j] = max(LCS[(i - 1) % 2][j], LCS[i % 2][j - 1])
return LCS[m % 2][n]Time and space complexity analysis
There are no changes in time complexity compared to the previous approach, as we are using two nested loops similar to the previous approach. Therefore, the time complexity remains O(mn). The space complexity, on the other hand, reduces to O(n) since the total number of rows is constant.
Efficient Space-Optimized Solution
Solution Idea and Steps
Now, the critical question is: Can we further optimize the space complexity? The idea is to store values in one row and track the previous row values (only 2 values) using two variables, instead of using a two-row 2-D table and storing values in a row-wise fashion. Let's think!
Step 1: We use a 1D array LCS[n] to store the values of the current row.
Step 2: We run nested loops similar to the last approach. At the ith iteration of the outer loop, we store ith-row values in the table LCS[] using an inner loop. Suppose after the (i - 1)th iteration of the outer loop, all the values of the (i - 1)th row are stored in the table. Now, we try to store the values of the ith row.
- We run the inner loop from j = 1 to n to fill table entries for the ith row. Before starting the inner loop, we initialize two variables PrevRow = 0 and preRowPrevCol = 0 to track two values of previous rows i.e. LCS[i-1][j] and LCS[i-1][j-1].
- Before storing the value at LCS[j], we update the variables PrevRow and preRowPrevCol, i.e., prevRowPrevCol = prevRow, prevRow = LCS[j]. Now we have the information to store the values at the position LCS[j].
- If (X[i-1] != Y[j-1]), LCS[j] = max(LCS[j-1], prevRow). Here prevRow is the value of the jth index in the (i-1)th iteration of the outer loop, and LCS[j-1] is the value of the (j-1)th index in the ith iteration of the outer loop.
- If (X[i-1] == Y[j-1]), LCS[j] = prevRowPrevCol + 1. Here prevRowPrevCol is the calculated value of the (j-1)th index in the (i-1)th iteration of the outer loop.
- We fill all the entries of the table LCS[n] by updating the values of both variables in a similar fashion.
Step 3: After filling the ith-row entries in the table, we move to the next iteration of the outer loop to fill the (i + 1)th row entries.
Step 4: By the end of both nested loops, our final solution gets stored at the position LCS[n]. We return this value as output.
We highly recommend visualizing this approach on paper.
Solution code C++
int lcs(string X[], string Y[], int m, int n)
{
int LCS[n + 1];
for (int i = 0; i <= n; i = i + 1)
LCS[i] = 0;
for (int i = 1; i <= m; i = i + 1)
{
int prevRow = 0, prevRowPrevCol = 0;
for (int j = 1; j <= n; j = j + 1)
{
prevRowPrevCol = prevRow;
prevRow = LCS[j];
if (X[i - 1] == Y[j - 1])
LCS[j] = prevRowPrevCol + 1;
else
LCS[j] = max(LCS[j - 1], prevRow);
}
}
return LCS[n];
}Solution code Python
def lcs(X, Y, m, n):
LCS = [0] * (n + 1)
for i in range(1, m + 1):
prev_row = 0
prev_row_prev_col = 0
for j in range(1, n + 1):
prev_row_prev_col = prev_row
prev_row = LCS[j]
if X[i - 1] == Y[j - 1]:
LCS[j] = prev_row_prev_col + 1
else:
LCS[j] = max(LCS[j - 1], prev_row)
return LCS[n]Time and space complexity analysis
There is no change in time complexity as we use two nested loops similar to the previous approach. So the time complexity is O(mn). The space complexity is still O(n), but it is an optimized version of the previous approach because we only use a 1D table to store one row.
Critical ideas to think about!
- Is it possible to solve the problem by comparing the first characters of strings instead of the last characters? If so, how can we store the solutions in the table?
- How can we modify all approaches to also return one of the longest subsequences? What is the time and space complexity for this modification? Can we modify the code to return the longest subsequence in lexicographical order?
- Can we implement the space-optimized approach using two separate arrays of size n?
- In the last two space-optimized approaches, what is the best version of the space complexity when n is greater than m? How can we modify the code so that the space complexity becomes O(m)?
- In the last four approaches, can we use hash tables to store the solutions to smaller subproblems instead of using an array?
- What are the worst and best-case scenarios for the brute force recursive approach?
Application of longest common subsequence problem
Molecular biology: DNA sequences, also known as genes, can be represented as sequences of four letters (A, C, G, and T) that correspond to the four sub-molecules that make up DNA. When biologists discover a new sequence, they often want to know which other sequences are the most similar. One way to determine the similarity of two sequences is to find the length of their longest common subsequence.
File comparison: The Unix program "diff" is used to compare two different versions of the same file to identify any changes made to the file. It does this by finding the longest common subsequence of the lines of the two files. Any line in the subsequence has not been changed, so the program displays the remaining set of lines that have been modified. In this problem, we can think of each file line as a single, complex character in a string.
Suggested coding questions to practice
- Edit distance problem
- Shortest common super-sequence
- Wildcard pattern matching
- Longest palindromic subsequence
- The maximum length of the repeated subarray
Content References
- Algorithms by CLRS
- Algorithm Design Manual by Skiena
If you have any queries/doubts/feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!
