Print a Given Matrix in Spiral Form

Difficulty: Medium, Asked-in: Amazon, Microsoft

Key takeaway: An excellent matrix problem to learn problem-solving using both iteration and recursion.

Let’s understand the problem

Given a 2-dimensional m x n matrix, print all the elements in spiral order.

Example 1

Input Matrix

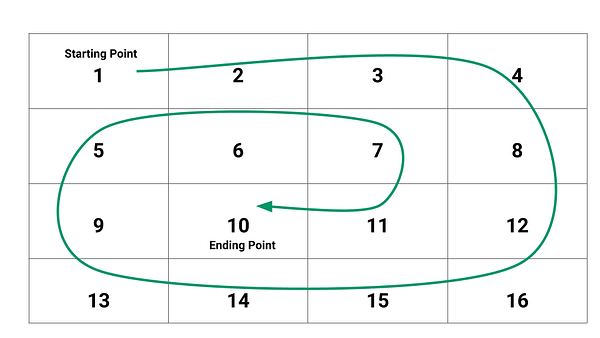
Output: 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10

Example 2

Input Matrix

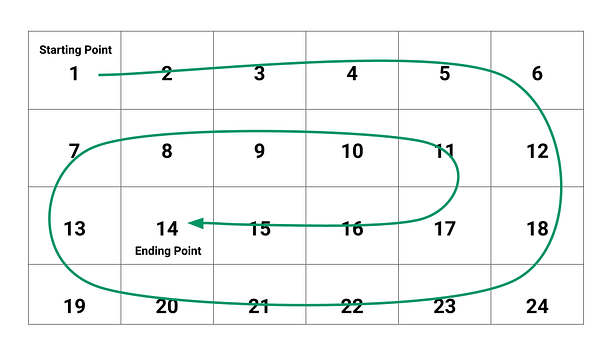
Output: 1 2 3 4 5 6 12 18 24 23 22 21 20 19 13 7 8 9 10 11 17 16 15 14

Discussed solution approaches

• Iterative approach using nested loops and variables
• Recursive approach using decrease and conquer

Iterative approach using nested loops and variables

Solution idea

We can imagine the spiral traversal as an ordered set of matrix segments with horizontal and vertical boundaries. Here are two critical observations from the output pattern:

Observation 1: During the spiral traversal, horizontal and vertical boundaries are reduced by one. In other words, it is one row and column shorter than the boundaries of the previous segment.

Observation 2: Boundaries of each next segment starts in a cell adjacent to the cell where the previous segment ends.

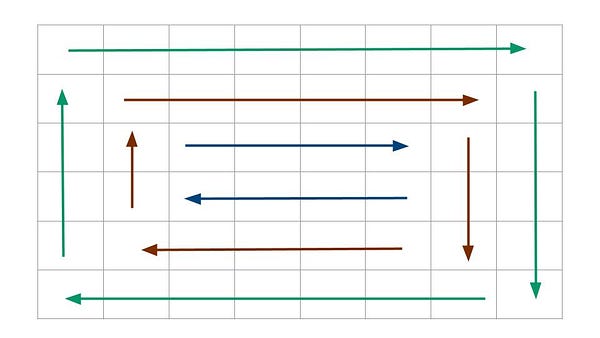
The idea is to solve the problem by dividing the matrix into segments with horizontal and vertical boundaries. It is visible that elements in the outer segment are printed in a clockwise manner, and then we move to the next segment and print elements in a similar way. So, we can imagine each segment as four boundaries, namely rowStart, colStart, rowEnd, and colEnd.

• rowStart: start row of the matrix segment where we move from left to right.
• colEnd: end column of the matrix segment where we move from top to down.
• rowEnd: end row of the matrix segment where we move from right to left.
• colStart: start column of the matrix segment where we move from down to up.

We can use a nested loop for the implementation: an outer loop to traverse each matrix segment and four inner loops to print each element in the segments in a clockwise manner. After each iteration, we reduce the horizontal and vertical boundary size by 1. For example, after traversing the outermost segment, the boundaries of the next segment will be rowStart + 1, colEnd - 1, rowEnd -1, and colStart + 1.

Solution steps

Step 1: We declare and initialize four variables to traverse matrix boundaries: rowStart = 0, , rowEnd = m - 1, colStart = 0, colEnd = n - 1.

Step2: We run an outer loop to access each segment, where the loop will end when we reach the innermost segment. In other words, loop will run till rowStart <= rowEnd and colStart <= colEnd. Think! We start from the first segment.

• We first print the top boundary from the colStart to the colEnd and increment the value of rowStart to shift the top boundary to the next segment.

  for (int i = colStart; i <= colEnd; i = i + 1)
    print(X[rowStart][i])
            
  rowStart = rowStart + 1

• Now we print the right boundary from rowStart to rowEnd and decrement the value of colEnd to shift the right boundary to the next segment.

  for (int i = rowStart; i <= rowEnd; i = i + 1)
    print(X[i][colEnd])
            
  colEnd = colEend - 1

• Now we print the bottom boundary from colEnd to colStart and decrement the value of rowEnd to shift the bottom boundary to the next segment. Boundary condition: In the first step, we have increased the rowStart by 1, so there can be a chance that the matrix segment will get reduced to one row i.e. both top and bottom boundaries are the same. So we only print the bottom boundary if(rowStart <= rowEnd). Think!

  if (rowStart <= rowEnd)
  {
    for (int i = colEnd; i >= colStart; i = i - 1)
        print(X[rowEnd][i])
                
    rowEnd = rowEnd - 1
  }

• Finally, we print the left boundary from rowEnd to rowStart and increment the value of colStart to shift the left boundary to the next segment. Boundary condition: In the second step, we have reduced the colEnd by 1, so there can be a chance that the matrix segment will get reduced to one column i.e. both left and right boundaries are the same. So we only print the left boundary if(colStart <= colEnd).

  if (colStart <= colEnd)
  {
    for (int i = rowEnd; i >= rowStart; i = i - 1)
        print(X[i][colStart])
                
    colStart = colStart + 1
  }

• At this point, we have printed the outermost segment and updated the variables in such a way that we can repeat the same procedure for the inner loops.

Step3: By end of the outer loop, our whole matrix gets printed in spiral order.

Solution pseudocode

void printSpiralOrder(int X[][], int m, int n)
{
    int rowStart = 0, rowEnd = m - 1 
    int colStart = 0, colEnd = n - 1 
    
    while(rowStart <= rowEnd && colStart <= colEnd)
    {
        for (int i = colStart; i <= colEnd; i = i + 1)
            print(X[rowStart][i])
        
        rowStart = rowStart + 1
        
        for (int i = rowStart; i <= rowEnd; i = i + 1)
            print(X[i][colEnd])
         
        colEnd = colEend - 1
        
        if (rowStart <= rowEnd)
        {
            for (int i = colEnd; i >= colStart; i = i - 1)
                print(X[rowEnd][i])
            
            rowEnd = rowEnd - 1
        }
        
        if (colStart <= colEnd)
        {
            for (int i = rowEnd; i >= rowStart; i = i - 1)
                print(X[i][colStart])
            
            colStart = colStart + 1
        }
    }
}

Implementation code C++

#include <iostream>
using namespace std;

#define Row 4
#define Col 4

void printSpiralOrder(int X[Row][Col], int m, int n)
{
    int rowStart = 0, rowEnd = m - 1;
    int colStart = 0, colEnd = n - 1;
    
    while (rowStart <= rowEnd && colStart <= colEnd)
    {
        for (int i = colStart; i <= colEnd; i = i + 1)
            cout << X[rowStart][i] << " ";
        
        rowStart = rowStart + 1;
        
        for (int i = rowStart; i <= rowEnd; i = i + 1)
            cout << X[i][colEnd] << " ";
        
        colEnd = colEnd - 1;
        
        if (rowStart <= rowEnd)
        {
            for (int i = colEnd; i >= colStart; i = i - 1)
                cout << X[rowEnd][i] << " ";
              
            rowEnd = rowEnd - 1;
        }
        
        if (colStart <= colEnd)
        {
            for (int i = rowEnd; i >= rowStart; i = i - 1)
                cout << X[i][colStart] << " ";
            
            colStart = colStart + 1;
        }
    }
}

int main()
{
    // Driver code
    int X[Row][Col] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16} };
    printSpiralOrder(X, Row, Col);
    // Output = 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
    return 0;
}

Implementation code Python

def printSpiralOrder(X, m, n):
    rowStart = 0
    rowEnd = m - 1
    colStart = 0
    colEnd = n - 1

    while rowStart <= rowEnd and colStart <= colEnd:
        for i in range(colStart, colEnd + 1):
            print(X[rowStart][i], end =' ')
        rowStart = rowStart + 1

        for i in range(rowStart, rowEnd + 1):
            print(X[i][colEnd], end=' ')
        colEnd = colEnd - 1

        if rowStart <= rowEnd:
            for i in range(colEnd, colStart - 1, -1):
                print(X[rowEnd][i], end =' ')
            rowEnd = rowEnd - 1

        if colStart <= colEnd:
            for i in range(rowEnd, rowStart - 1, -1):
                print(X[i][colStart], end =' ')
            colStart = colStart + 1

Implementation code Java

class Solution
{
    public void printSpiralOrder(int[][] X, int m, int n) 
    {
        int rowStart = 0;
        int rowEnd = m - 1;
        int colStart = 0;
        int colEnd = n - 1;

        while (rowStart <= rowEnd && colStart <= colEnd) 
        {
            for (int i = colStart; i <= colEnd; i =  i + 1)
                System.out.print(X[rowStart][i] + " ");

            rowStart = rowStart + 1;

            for (int i = rowStart; i <= rowEnd; i = i + 1)
                System.out.print(X[i][colEnd] + " ");
                
            colEnd = colEnd - 1;

            if (rowStart <= rowEnd) 
            {
                for (int i = colEnd; i >= colStart; i = i - 1)
                    System.out.print(X[rowEnd][i] + " ");
                
                rowEnd = rowEnd - 1;
            }

            if (colStart <= colEnd) 
            {
                for (int i = rowEnd; i >= rowStart; i = i - 1)
                    System.out.print(X[i][colStart] + " ");
                
                colStart = colStart + 1;
            }
        }
    }
}

Time and space complexity analysis

We are traversing each element of the matrix once. Time complexity = O(n*m), Space complexity = O(1)

Recursive approach using decrease and conquer

Solution idea

Can we think to solve this problem recursively? The idea is to visualize the problem solution via the solution of the smaller problem. Let's think!

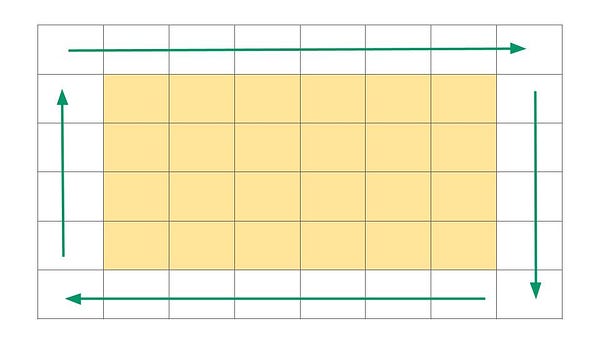
Suppose we have a given matrix of dimension m x n to print in the spiral order. After printing the outermost boundary using four loops, now the problem gets reduced to a smaller version of the same problem: printing the inner matrix of dimension (m-2)x(n-2). We can use variables rowStart, colStart, rowEnd, and colEnd to track the matrix dimension during the recursion.

Solution steps

We are using function printSpiralOrder(). Inside the function, we initialize all the variables and make a call to the helper unction recursiveSpiral() to print the matrix in spiral order.

void printSpiralOrder(int X[][], int m, int n)
{
    int rowStart = 0, rowEnd = m - 1 
    int colStart = 0, colEnd = n - 1 
    recursiveSpiral(X, rowStart, rowEnd, colStart, colEnd)
}

Implementation of the recursiveSpiral(X[], rowStart, rowEnd, colStart, colEnd)

Step 1: We first traverse the outermost boundary using four loops similar to the loop used in the iterative implementation.

• Print the first row using a loop from colStart to colEnd.
• Print the last column using a loop from rowStart + 1 to rowEnd.
• Print the last row using a loop from colEnd - 1 to colStart. Before doing this, we need to check if the last and the first row are not the same.
• Print the first column using a loop from rowEnd - 1 to rowStart + 1. Before doing this, we need to check, if the last and the first column are not the same.

Step2: Now we print the remaining matrix recursively using the same function with the updated boundary parameters i.e rowStart + 1, colStart + 1, rowEnd - 1, and colEnd - 1.

Base condition: Recursion will stop in any one of the two conditions: rowStart > rowEnd or colStart > colEnd.

Solution pseudocode

void recursiveSpiral(int X[][], int rowStart, int rowEnd, int colStart, int colEnd)
{
    if (rowStart > rowEnd || colStart > colEnd)
        return
    
    for (int i = colStart; i <= colEnd; i = i + 1)
        print(X[rowStart][i])
        
    for (int i = rowStart + 1; i <= rowEnd; i = i + 1)
        print(X[i][colEnd])
        
    if (rowEnd != rowStart)
    {
        for (int i = colEnd - 1; i >= colStart; i = i - 1)
            print(X[rowEnd][i])
    }
        
    if (colEnd != colStart)
    {
        for (int i = rowEnd - 1; i >= rowStart + 1; i = i - 1)
            print(X[i][colStart])
    }
    
    recursiveSpiral(X, rowStart + 1, rowEnd - 1, colStart + 1, colEnd - 1)
}

Implementation code C++

#include <iostream>
using namespace std;
#define Row 4
#define Col 4

void recursiveSpiral(int X[Row][Col], int rowStart, int rowEnd, int colStart, int colEnd)
{
    if (rowStart > rowEnd || colStart > colEnd)
        return;
    
    for (int i = colStart; i <= colEnd; i = i + 1)
        cout << X[rowStart][i] << " ";
        
    for (int i = rowStart + 1; i <= rowEnd; i = i + 1)
        cout << X[i][colEnd] << " ";
        
    if (rowEnd != rowStart)
    {
        for (int i = colEnd - 1; i >= colStart; i = i - 1)
            cout << X[rowEnd][i] << " ";
    }
        
    if (colEnd != colStart)
    {
        for (int i = rowEnd - 1; i >= rowStart + 1; i = i - 1)
            cout << X[i][colStart] << " ";
    }
    
    recursiveSpiral(X, rowStart + 1, rowEnd - 1, colStart + 1, colEnd - 1);
}

void printSpiralOrder(int X[Row][Col], int m, int n)
{
    int rowStart = 0, rowEnd = m - 1;
    int colStart = 0, colEnd = n - 1;
    recursiveSpiral(X, rowStart, rowEnd, colStart, colEnd);
}

int main()
{
    // Driver code
    int X[Row][Col] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16} };
    printSpiralOrder(X,Row, Col);
    // Output = 1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10 
    return 0;
}

Implementation code Python

def recursiveSpiral(X, rowStart, rowEnd, colStart, colEnd):
    if rowStart > rowEnd or colStart > colEnd:
        return
    
    for i in range(colStart, colEnd + 1):
        print(X[rowStart][i], end =' ')
        
    for i in range(rowStart + 1, rowEnd + 1):
        print(X[i][colEnd], end =' ')
        
    if rowEnd != rowStart:
        for i in range(colEnd - 1, colStart - 1, -1):
            print(X[rowEnd][i], end =' ')
        
    if colEnd != colStart:
        for i in range(rowEnd - 1, rowStart, -1):
            print(X[i][colStart], end =' ')
    
    recursiveSpiral(X, rowStart + 1, rowEnd - 1, colStart + 1, colEnd - 1)
 
def printSpiralOrder(X, m, n):
    rowStart = 0
    rowEnd = m - 1
    colStart = 0
    colEnd = n - 1
    recursiveSpiral(X, rowStart, rowEnd, colStart, colEnd)

Implementation code Java

class Solution 
{
    private void recursiveSpiral(int[][] X, int rowStart, int rowEnd, int colStart, int colEnd) 
    {
        if (rowStart > rowEnd || colStart > colEnd) 
            return;
    
        for (int i = colStart; i <= colEnd; i = i + 1)
            System.out.print(X[rowStart][i] + " ");
        
        for (int i = rowStart + 1; i <= rowEnd; i = i + 1)
            System.out.print(X[i][colEnd] + " ");
        
        if (rowEnd != rowStart) 
        {
            for (int i = colEnd - 1; i >= colStart; i = i - 1)
                System.out.print(X[rowEnd][i] + " ");
        }
        
        if (colEnd != colStart) 
        {
            for (int i = rowEnd - 1; i >= rowStart + 1; i = i - 1)
                System.out.print(X[i][colStart] + " ");
        }
    
        recursiveSpiral(X, rowStart + 1, rowEnd - 1, colStart + 1, colEnd - 1);
    }
    
    public void printSpiralOrder(int[][] X, int m, int n) 
    {
        int rowStart = 0, rowEnd = m - 1;
        int colStart = 0, colEnd = n - 1;
        recursiveSpiral(X, rowStart, rowEnd, colStart, colEnd);
    }
}

Time and space complexity analysis

In the above solution, there is no need to do analysis by writing recurrence relation and solving it using the recursion tree method! The idea of analysis would be simple: we are printing each element of the matrix and performing an O(1) operation for each element. So time complexity = m*n*O(1) = O(mn).

Space complexity depends on the size of the call stack which is equal to the depth of the recursion. Here input size is decreasing by the factor of 2 at each step of recursion i.e both m and n are decreasing by 2. So the depth of the recursion depends on the minimum of m and n.

• If m > n, depth of the recursion = n/2.
• If m < n, depth of the recursion = m/2.

So space complexity = O(min(m, n)). Think!

Critical ideas to think!

• Explain the boundary situation when there is a single row or single column in the matrix. Before running last two inner loops, Why are we checking the condition if(rowStart < rowEnd) and if(colStart < colEnd)?
• Can we solve this problem using some other approach?
• How do we modify the logic if we need to print the matrix in reverse spiral order i.e. anticlockwise direction?
• Try to explore the analysis of recursive solutions using the recursion tree method.

Comparisons of time and space complexities

• Using iterative approach: Time = O(mn), Space = O(1).
• Using recursive approach: Time = O(mn), Space = O(max(m, n).

Matrix-based problems to practice

• Rotate a matrix by 90 degrees
• Find row with max ones
• Transpose matrix
• Set matrix zeroes
• 01 Matrix
• Reshape the matrix
• Toeplitz Matrix

If you have any queries or feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!