Implement Stack using Queues

Difficulty: Easy, Asked-in: Microsoft, Amazon, Adobe

Key takeaway: An excellent problem to visualize the use case of stack and queue operations.

Let’s understand the problem

Write a program to implement a stack using the queues. The implemented stack should support standard push(x) and pop() operations.

• void push(int x): Insert an element x to the top of the stack.
• int pop(): Remove an element from the top of the stack and return it.

Problem notes

• Stack is a last-in-first-out (LIFO) data structure, in which elements are added and removed from the top end. In contrast, the queue is a first-in-first-out (FIFO) data structure, in which elements are added from one end (back) and removed from the other end(front).
• We must use only standard queue operations.

Discussed solution approaches

• Using two queues: O(n) pop operation and O(1) push operation
• Using two queues: O(1) pop operation and O(n) push operation
• Using a single queue: O(1) pop operation and O(n) push operation

Using two queues: O(n) pop operation and O(1) push operation

We can understand the basic idea for implementing a stack using a queue by considering the order of insertion and deletion in both data structures. In a stack, we insert and delete elements from one end only, but in a queue, we insert elements at the back and delete elements from the front. Therefore, to simulate a stack using a queue, we need to keep track of the last element inserted and make sure that it is the first element to be deleted. This can be achieved by manipulating the order of the elements in the queue.

Suppose we use a single queue to implement a stack. In this case, we can perform a push operation by simply inserting the new element at the back of the queue. However, if we want to perform a pop operation, we need to remove the last element inserted into the queue, which is at the back of the queue. But the queue is a first-in, first-out (FIFO) data structure, which means we can only remove elements from the front of the queue. The key question here is: how do we remove the element at the back of the queue?

One solution to this problem could be to continuously remove elements from the queue until we reach the element at the back. This would mean removing all the elements in the queue except for the last element, which is the top element of the stack. However, before removing the last element, we need to store and maintain the order of the removed elements for future use. To do this, we can use an additional queue to store the removed elements. Therefore, to perform the pop operation using a single queue, we need to use two queues.

Suppose we define a class called StackUsingQueue to implement a stack using queues. Inside this class:

• We declare two queues, Q1 and Q2, to simulate stack operations.
• We declare a variable called stackSize to track the current size of the stack.
• We define methods for stack operations: void push(int x) and int pop().

Implementation of the push operation

To add a new element to the stack, we enqueue it to the first queue, Q1. This means we insert the element x at the back of queue Q1, which will become the top element of the stack. After inserting the element, we increment the value of stackSize by 1 to track the current size of the stack.

Implementation pseudocode

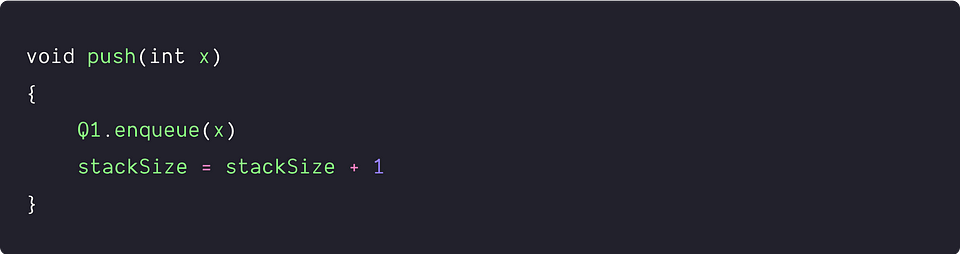
We are performing a constant number of operations i.e. only one enqueue operation. So time complexity = O(1).

Implementation of the pop operation

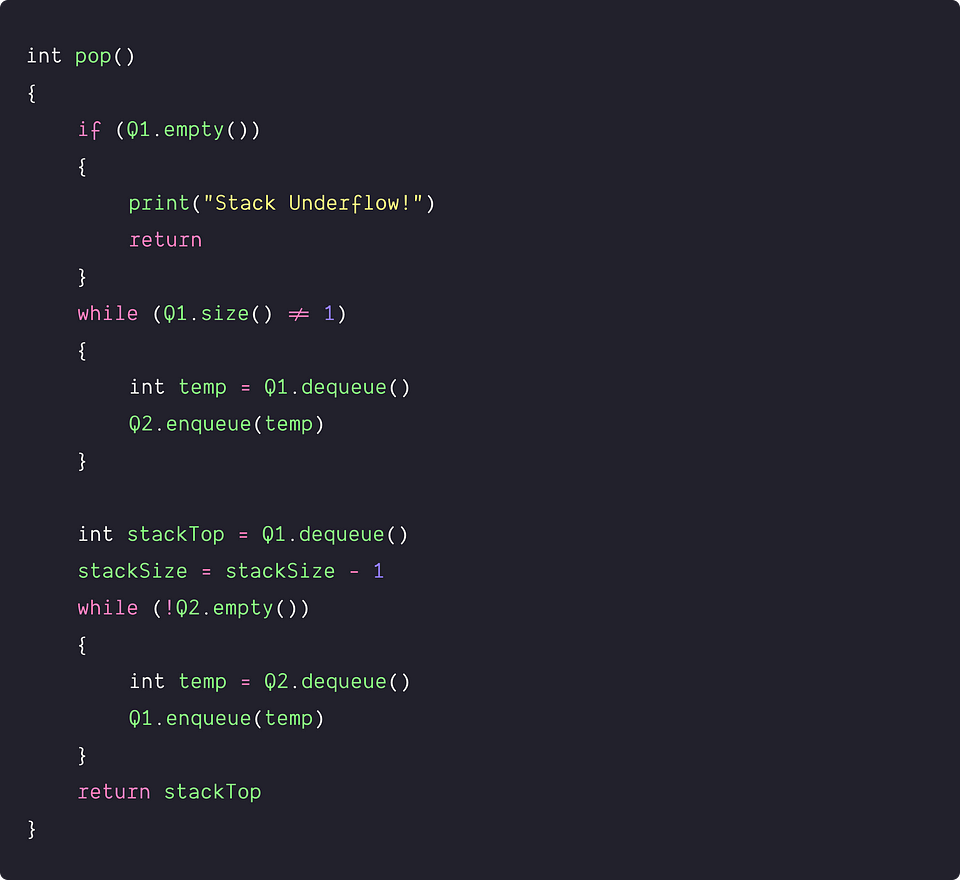
As previously mentioned, to perform the pop operation, our goal is to remove the last element inserted into queue Q1 using another queue, Q2. To achieve this, we can follow the following steps.

• If queue Q1 is empty, we throw an error message "stack underflow" and return. Otherwise, we run a loop until there is only one element left in queue Q1. In this loop, we dequeue each element from queue Q1 and enqueue it into queue Q2.
• We dequeue the last remaining element in queue Q1 and store it in a variable called stackTop. We also decrement the value of stackSize by 1 to reflect the new size of the stack.
• Then, we run a loop until queue Q2 is empty and move all the elements from queue Q2 to queue Q1.
• Finally, we return the value stored in the variable stackTop as the output of the pop operation.

Implementation pseudocode

Optimized implementation of the pop operation

The critical question is: in the 3rd step of the pop operation, do we really need to move all the elements from Q2 to Q1? If we observe closely, the answer is no: the Q1 will be empty at that stage, and elements in Q2 are in the same order as earlier in Q1. So rather than moving elements from Q2 to Q1, we just need to swap the reference of Q1 with Q2.

Implementation pseudocode

The algorithm dequeues n elements from Q1 and enqueues n − 1 element to Q2, where n is the size of the stack. So total number of queue operations = 2n − 1 and time complexity = O(n).

Note: It's an exercise for you to design an efficient algorithm for the top() operation.

Implementation code C++

class StackUsingQueue
{
private:
    queue<int> Q1, Q2;
    int stackSize;

public:
    StackUsingQueue()
    {
        stackSize = 0;
    }

    void push(int x)
    {
        Q1.push(x);
        stackSize = stackSize + 1;
    }

    int pop()
    {
        if (Q1.empty())
        {
            cout << "Stack Underflow!" << endl;
            return INT_MIN;
        }

        while (Q1.size() != 1)
        {
            int temp = Q1.front();
            Q1.pop();
            Q2.push(temp);
        }

        int stackTop = Q1.front();
        Q1.pop();
        stackSize = stackSize - 1;
        swap(Q1, Q2);
        return stackTop;
    }
};

Implementation code Python

class StackUsingQueue:
    def __init__(self):
        self.Q1 = deque()
        self.Q2 = deque()
        self.stack_size = 0

    def push(self, x):
        self.Q1.append(x)
        self.stack_size = self.stack_size + 1

    def pop(self):
        if not self.Q1:
            print("Stack Underflow!")
            return -sys.maxsize

        while len(self.Q1) != 1:
            temp = self.Q1.popleft()
            self.Q2.append(temp)

        stack_top = self.Q1.popleft()
        self.stack_size = self.stack_size - 1
        self.Q1, self.Q2 = self.Q2, self.Q1
        return stack_top

Implementation code Java

class StackUsingQueue
{
    private Queue<Integer> Q1, Q2;
    private int stackSize;

    public StackUsingQueue()
    {
        Q1 = new LinkedList<>();
        Q2 = new LinkedList<>();
        stackSize = 0;
    }

    public void push(int x)
    {
        Q1.add(x);
        stackSize = stackSize + 1;
    }

    public int pop()
    {
        if (Q1.isEmpty())
        {
            System.out.println("Stack Underflow!");
            return Integer.MIN_VALUE;
        }

        while (Q1.size() != 1)
        {
            int temp = Q1.poll();
            Q2.add(temp);
        }

        int stackTop = Q1.poll();
        stackSize = stackSize - 1;
        Queue<Integer> temp = Q1;
        Q1 = Q2;
        Q2 = temp;
        return stackTop;
    }
}

Using two queues: O(1) pop operation and O(n) push operation

Now the critical question is: can we think of another implementation similar to the above approach but in a reverse way i.e. O(1) pop and O(n) push operation? Let's think!

Implementation of the pop operation

Here the idea is to maintain the front element of the queue as the top element of the stack. So, for removing an element from the stack, we simply dequeue the front element from Q1.

Implementation pseudocode

• We are performing a constant number of operations i.e. only one dequeue operation. So time complexity = O(1)
• We are using constant extra space. So space complexity = O(1)

Implementation of the push operation

The new element is always inserted at the back of the queue. But for maintaining the stack order, we need to position the new element at the front of the queue. How do we do it? Let's think!

• We first move all elements from Q1 to Q2.
• Then we enqueue the new element x to the Q1.
• Now move all elements from Q2 to Q1. This ensures that the new element would be in the front of Q1. When we perform the next pop operation, we can easily access the new element from the front of the Q1.

Implementation pseudocode

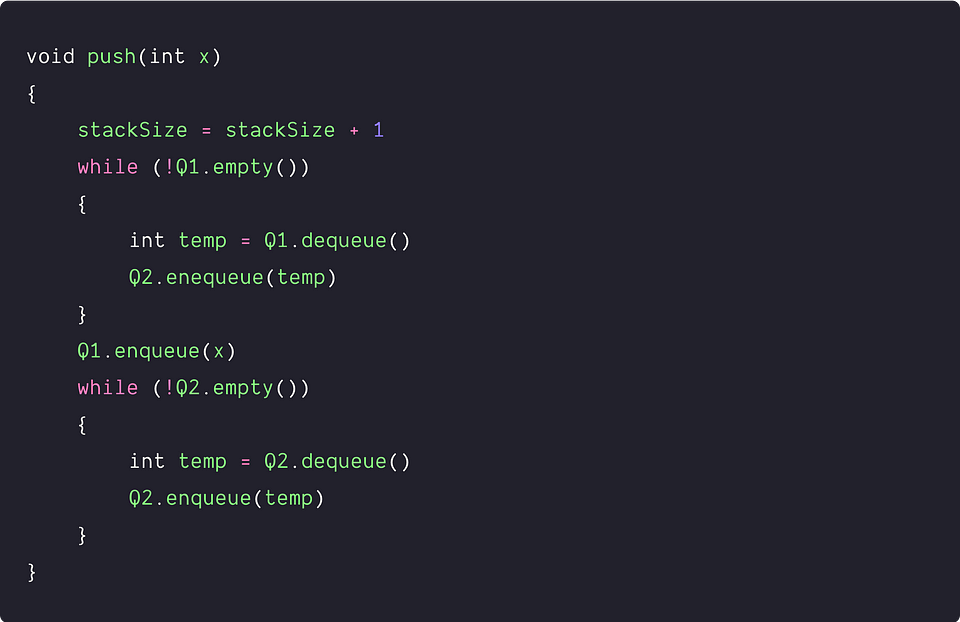
Optimized implementation of the push operation

In the 3rd step of the push operation, there is no need to copy all the elements from Q2 to Q1. We have already discussed a similar idea for the pop operation in the above approach.

• We enqueue new element x to the empty queue Q2.
• Now we first move all elements from Q1 to Q2.
• After this, the new element will be present at the front of Q2 and Q1 is empty. So rather than copy elements from Q2 to Q1, we need to just swap the references of Q1 and Q2.

Implementation pseudocode

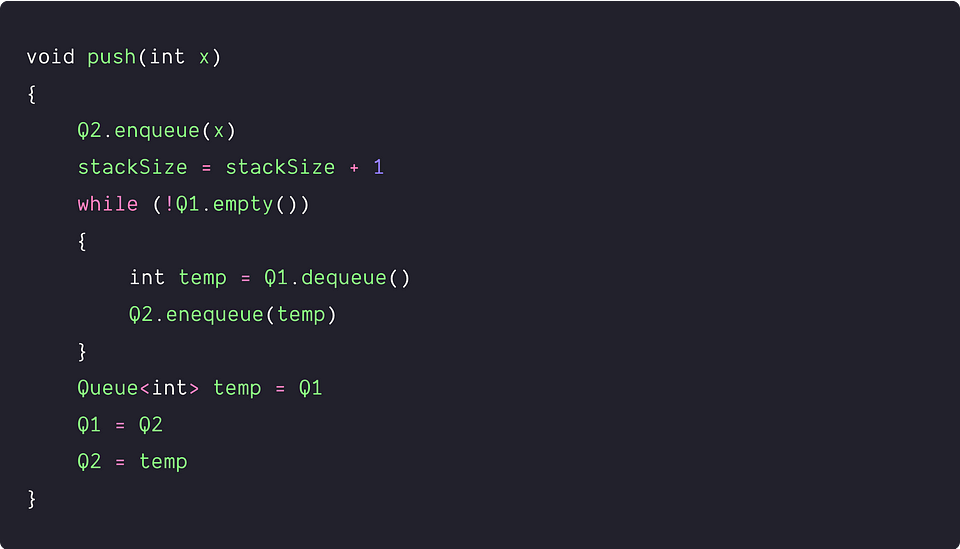
• The algorithm removes n elements from Q1 and inserts n + 1 elements to Q2, where n is the size of the stack. So total number of queue operations = 2n + 1. Time complexity = O(n).
• Space complexity = O(1)

Note: It's an exercise for you to design an efficient algorithm for the top() operation.

Implementation code C++

class StackUsingQueue
{
    queue<int> Q1, Q2;
    int stackSize;

public:
    StackUsingQueue() 
    { 
        stackSize = 0;
    } 
    
    void push(int x)
    {
        Q2.push(x);
        stackSize = stackSize + 1;
        while (!Q1.empty()) 
        {
            int temp = Q1.front();
            Q1.pop();
            Q2.push(temp);
        }
        queue<int> temp = Q1;
        Q1 = Q2;
        Q2 = temp;
    }
 
    int pop()
    {
        if (Q1.empty()) 
        {
            cout << "Stack Underflow!!" << endl;
            return -1;
        }
        int stackTop = Q1.front();
        Q1.pop();
        stackSize = stackSize - 1;
        return stackTop;
    }
};

Implementation code Python

class StackUsingQueue:
    def __init__(self):
        self.Q1 = []
        self.Q2 = []
        self.stackSize = 0

    def push(self, x):
        self.Q2.append(x)
        self.stackSize = self.stackSize + 1
        while len(self.Q1) > 0:
            temp = self.Q1.pop(0)
            self.Q2.append(temp)
        self.Q1, self.Q2 = self.Q2, self.Q1

    def pop(self):
        if len(self.Q1) == 0:
            print("Stack Underflow!!")
            return -sys.maxsize
        stackTop = self.Q1.pop(0)
        self.stackSize = self.stackSize - 1
        return stackTop

Implementation code Java

class StackUsingQueue
{
    Queue<Integer> Q1, Q2;
    int stackSize;

    public StackUsingQueue() 
    { 
        stackSize = 0;
        Q1 = new LinkedList<>();
        Q2 = new LinkedList<>();
    } 
    
    public void push(int x)
    {
        Q2.add(x);
        stackSize = stackSize + 1;
        while (!Q1.isEmpty()) 
        {
            int temp = Q1.poll();
            Q2.add(temp);
        }
        Queue<Integer> temp = Q1;
        Q1 = Q2;
        Q2 = temp;
    }
 
    public int pop()
    {
        if (Q1.isEmpty()) 
        {
            System.out.println("Stack Underflow!!");
            return Integer.MIN_VALUE;
        }
        int stackTop = Q1.poll();
        stackSize = stackSize - 1;
        return stackTop;
    }
}

Using a single queue: O(1) pop operation and O(n) push operation

The above approaches use two queues. Now the critical question is: Can we optimize the implementation using a single queue? Let's think!

Suppose for the pop operation; we always insert elements at the front of the queue to get access in constant time. Now for the push operation, if we insert an element in the queue, it will be stored at the back of the queue due to the queue properties. But we need the last inserted element to the front of the queue to remove it first in the next pop operation. One idea would be to: after pushing the new element, we need to reverse the order of the remaining queue elements. So we can use only one queue to implement the stack.

Implementation of the pop operation

For removing an element from the stack, we simply dequeue the front element from Q. This is similar to the previous approach.

Implementation pseudocode

• We are performing a constant number of operations i.e. only one dequeue operation. So time complexity = O(1)
• We are using constant extra space. So space complexity = O(1)

Implementation of the push operation

The idea is to first add the new element, x, to the queue. Then, we reverse the order of the elements in the queue by repeatedly removing each element from the front of the queue (except for the last element) and adding it back to the end. In other words, this process continues until there is only one element left in the queue.

Implementation pseudocode

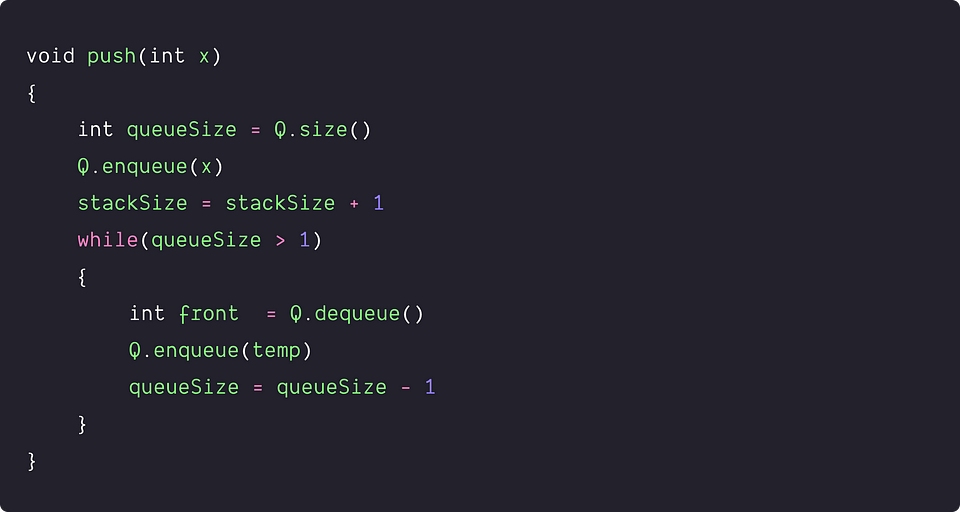
The algorithm removes n elements and inserts n + 1 elements to Q, where n is the stack size. So total number of queue operations = 2n + 1. Time complexity = O(n).

Implementation code C++

class StackUsingQueue
{
    queue<int> Q;
    int stackSize;

public:
    StackUsingQueue() 
    { 
        stackSize = 0;
    } 
    
    void push(int x)
    {
        int queueSize = Q.size();
        Q.push(x);
        stackSize = stackSize + 1;
        while (queueSize > 1) 
        { 
            int temp = Q.front();
            Q.pop();
            Q.push(temp);
            queueSize = queueSize - 1;
        } 
    }
    
    int pop()
    {
        if (Q.empty()) 
        {
            cout << " Stack Underflow!" << endl;
            return INT_MIN;
        }
        int stackTop = Q.front();
        Q.pop();
        stackSize = stackSize - 1;
        return stackTop;
    }
};

Implementation code Python

class StackUsingQueue:
    def __init__(self):
        self.Q = []
        self.stackSize = 0

    def push(self, x):
        queueSize = len(self.Q)
        self.Q.append(x)
        self.stackSize = self.stackSize + 1
        while queueSize > 1: 
            temp = self.Q[0]
            self.Q.pop(0)
            self.Q.append(temp)
            queueSize = queueSize - 1

    def pop(self):
        if len(self.Q) == 0:
            print(" Stack Underflow!")
            return -sys.maxsize
        stackTop = self.Q[0]
        self.Q.pop(0)
        self.stackSize = self.stackSize - 1
        return stackTop

Implementation code Java

class StackUsingQueue 
{
    Queue<Integer> Q;
    int stackSize;

    public StackUsingQueue() 
    {
        Q = new LinkedList<>();
        stackSize = 0;
    }

    public void push(int x) 
    {
        int queueSize = Q.size();
        Q.add(x);
        stackSize = stackSize - 1;
        while (queueSize > 1) 
        {
            int temp = Q.poll();
            Q.add(temp);
            queueSize = queueSize - 1;
        }
    }

    public int pop() 
    {
        if (Q.isEmpty()) 
        {
            System.out.println(" Stack Underflow!");
            return Integer.MIN_VALUE;
        }
        int stackTop = Q.poll();
        stackSize = stackSize - 1;
        return stackTop;
    }
}

Critical ideas to think!

• Is it possible to implement a stack where each operation has an amortized time complexity of O(1)?
• How does the efficiency of the above approaches depend on the frequency of push and pop operations? If the push operation is much more frequent than the pop operation, which approach should be followed
• Can we consider designing alternative strategies to implement a stack using queues?
• Based on the complexity of enqueue or dequeue operations, which type of queue implementation would be most suitable for the above implementations - an array-based implementation or a linked list implementation?
• How do we implement the top() and isEmpty() operations in all of the above approaches? Is it possible to design a strategy to get the top element with an O(1) time complexity?

Suggested coding problems to practice

• Implement queue using stacks
• Min-stack problem
• Implement Stack and Queue using Deque
• Implement stack using a priority queue
• Sort a stack using a temporary stack
• Reverse a Stack using another Stack
• Find maximum in a stack

Please write in the message below if you find anything incorrect, or you want to share more insight, or you know some different approaches to solve this problem. Enjoy learning, Enjoy algorithms!