Validate Binary Search Tree (Check if Binary Tree is BST or not)

Difficulty: Easy, Asked-in: Microsoft, Google, Amazon, eBay, Adobe, Qualcomm, VMWare, Walmart

Key takeaway: An excellent problem to understand the properties of binary search trees and learn step-by-step optimization using various approaches.

Let’s understand the problem

Given the root of a binary tree, write a program to check whether it is a valid binary search tree (BST) or not. A BST is valid if it has the following properties:

• All nodes in the left subtree have values less than the node’s value.
• All nodes in the right subtree have values greater than the node’s value
• Both left and right subtrees are also binary search trees.

Examples

Discussed solution approaches

• A wrong solution approach!
• Brute force approach: Comparing each node value with the max of the left sub-tree and min of the right sub-tree.
• Optimized version of the brute force approach: Tracking min and the max range of values allowed for the subtree rooted at each node.
• Using inorder traversal and extra space
• An efficient approach: In-place solution using inorder traversal

Wrong solution approach!

An unclear understanding of this problem can lead to a wrong approach. For example, suppose we understood the BST property incorrectly and designed this solution: We visit each node recursively and compare value stored in each node with value stored on the left and right child. If the node value is greater than left child value or less than right child value, we return false. Otherwise, we recursively call the same function to verify BST for left and right sub-tree.

boolean isValidBST (TreeNode root)
{
    if (root == NULL)
        return true 
    
    if (root->left != NULL && root->left->value > root->value)
        return false 
    if (root->right != NULL && root->right->value < root->value)
        return false
        
    boolean left = isValidBST(root->left)
    boolean right = isValidBST(root->right) 
    if(left == true && right == true)
        return true
    else 
        return false
}

What is the mistake in above solution?

Based on the BST property, each node value must be greater than all nodes in the left sub-tree and less than all nodes in the right sub-tree. But above solution just check this property for the children of each node, not the entire left or right subtree. So this solution will give the wrong result for several input cases. Consider this example:

Solution 1: A brute force and correct approach

Solution idea

Now the critical question is: How can we fix the above solution? Here is an idea: A tree can not be BST if left subtree contains any value greater than node’s value and right subtree contains any value smaller than node’s value. In other words, node value must be greater than the maximum in left subtree and less than the minimum in right subtree. Note: In a BST, the rightmost node would be the node with the maximum value and the leftmost node would be the node with the minimum value.

Solution steps

• Base case: If (root == NULL ), return true.
• We find max in the left subtree and min in the right subtree using two helper functions i.e. leftMax = bstMax(root->left) and rightMax = bstMin(root->right).
• If leftMax > root->value or rightMax < root->value, then root node violates the BST property and we return false. 
• Otherwise, root node satisfies the BST property. So we recursively check that left and right subtree are correct BST or not. For this, we call the same function with root->left and root->right as input parameters.

boolean left = isValidBST(root->left)
boolean right = isValidBST(root->right)

• If both left and right are true, return true. Otherwise, return false. Think!

Solution pseudocode

boolean isValidBST(TreeNode root)
{
    if (root == NULL)
        return true
    int leftMax = bstMax(root->left)
    int rightMax = bstMin(root->right)
    if (leftMax > root->value || rightMax < root->value)
        return false
        
    boolean left = isValidBST(root->left)
    boolean right = isValidBST(root->right)
    
    if(left == true && right == true)
        return true
    else 
        return false
}
int bstMax(TreeNode root)
{
    while(root->right != NULL)
        root = root->right
    return root->value
}
int bstMin(TreeNode root)
{
    while(root->left != NULL)
        root = root->left
    return root->value
}

Time complexity analysis

We are traversing the tree recursively and calling bstMax(root->left) and bstMin(root->right) for each node. The worst-case time complexity of finding max in a BST = O(n), the worst-case time complexity of finding min in a BST = O(n). Think!

If we look closely, time complexity will depend on the tree structure. The worst-case situation will occur when tree is highly unbalanced i.e., either left-skewed (All nodes have a left child except the single leaf node) or a right-skewed tree (All nodes have a right child except the single leaf node). So worst-case time complexity to validate BST = n*O(n) = O(n^2).

The above code is recursive. So here are some critical questions for the learning purpose! We will add answers to these questions later in this blog.

• The best-case scenario will occur when tree is balanced.
• The recurrence relation for the worst case is T(n) = T(n - 1) + O(n)
• The recurrence relation for the best case is T(n) = 2T(n/2) + O(logn)
• Proof that the best case time complexity is O(n)! Hint: Use the first case of the master theorem.
• What would be the space complexity?

Solution 2: An optimized version of the brute force approach

We need to traverse some nodes several times in the above method. Can we think of solving this problem efficiently? Can we think of solving the problem without finding the max and min for each node?

Solution idea

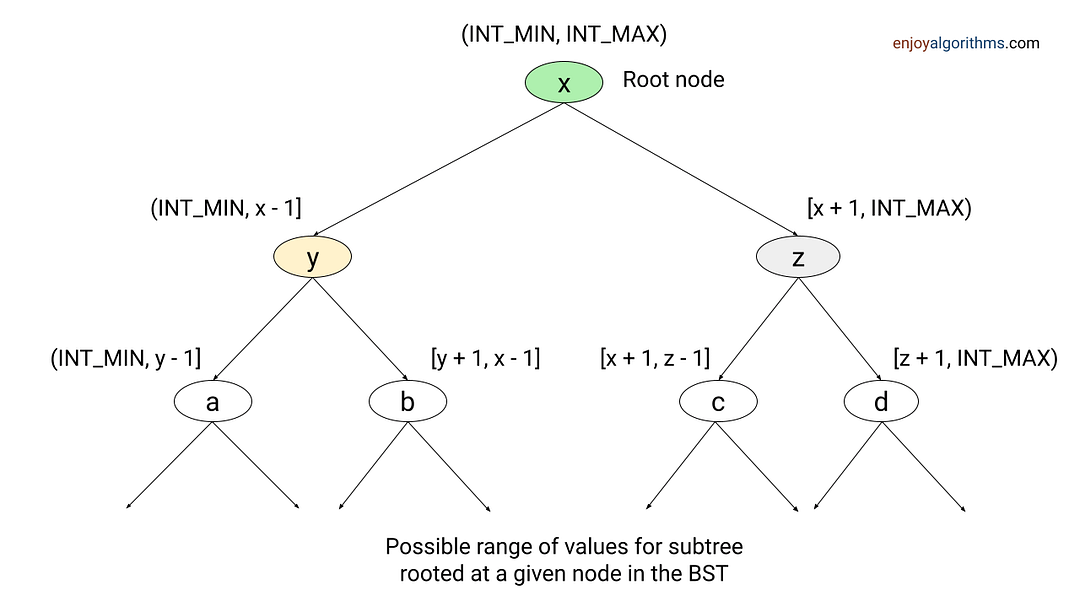
In BST, value stored in a subtree rooted at any node lies in a particular range. In other words, there is an upper (rangeMax) and a lower (rangeMin) limit of values that lie in a specific subtree. For example: 

• The tree with root node lies in the range (INTMIN, INTMAX).
• The left subtree lies in the range (INT_MIN, root-> value -1].
• Right subtree range is [root->value + 1, INT_MAX), and so on.

One solution would be to traverse the tree recursively and keep track of min and max range of values allowed for subtree rooted at each node. We pass the acceptable range as a function argument while recursing for the left and right subtree.

Here we need to go through each node only once, and the initial values for the min and max range should be INTMIN and INTMAX. If node->value < rangeMin or node->value > rangeMax, then node’s value falls outside the valid range and violates min-max constraints. So we return false. Otherwise, we recursively check left and right subtrees with an updated range.

Solution pseudocode

boolean isBST(TreeNode root)
{
    return isValidBST(root, INT_MIN, INT_MAX))
}
boolean isValidBST(TreeNode root, int rangeMin, int rangeMax)
{
    if(root == NULL)
        return true
    if (root->value < rangeMin || root->value > rangeMax)
        return false
        
    boolean left = isValidBST(root->left, rangeMin, root->value -1)
    boolean right = isValidBST(root->right, root->value + 1, rangeMax) 
    
    if(left == true && right == true)
        return true
    else 
        return false
}

Time and space complexity analysis

We visit each node only once and perform O(1) operation with each node. So time complexity = n* O(1) = O(n). Space complexity depends on the size of the recursion call stack, which is equal to the height of the tree. So space complexity = O(h). What would be the worst and best case of space complexity? Think!

Solution 3: Using inorder traversal and extra space

Solution idea

The inorder traversal of a binary search tree explores node values in sorted order. So another idea would be to traverse the tree using inorder traversal and store node values in an ArrayList or vector. Now we traverse the ArrayList or vector using a loop to check whether it is sorted or not. If sorted, then tree is a BST; otherwise, not.

Solution pseudocode

boolean isValidBST (TreeNode root)
{
    vector<int> sorted
    inorderTraversal(root, &sorted)
    for(int i = 1; i < sorted.size(); i = i + 1)
    {
        if (sorted[i] < sorted[i - 1])
            return false 
    }        
    return true
}
void inorderTraversal(TreeNode root, int & sorted)
{
    if (root == NULL)
        return
    inorderTraversal(root->left, sorted)
    sorted.push_back(root->value)
    inorderTraversal(root->right, sorted)
}

Time and space complexity analysis

Time complexity = Time complexity of inorder traversal for storing elements in array list + Time complexity of the single loop to check sorted array list = O(n) + O(n) = O(n). Space complexity = O(n) for storing elements in an array list + O(h) for recursion stack space = O(n + h)

Solution 4: In-place solution using inorder traversal

Solution idea

The critical question is: Can we think to optimize the above approach and avoid using extra space? As we know that inorder traversal of a BST returns the nodes in sorted order. So one idea would be to keep track of previously visited nodes while traversing the tree. If current node value is less than previous node value, then tree is not BST.

Solution pseudocode: Recursive inorder traversal

boolean isBST(TreeNode root)
{
    TreeNode prev = NULL
    return isValidBST(root, &prev)
}
boolean isValidBST(TreeNode root, TreeNode &prev) 
{
    if (root == NULL) 
        return true
    boolean left = isValidBST(root->left, prev)
    if (prev != NULL && root->value < prev->value) 
        return false
    prev = root
    boolean right = isValidBST(root->right, prev)
    if(left == true && right == true)
        return true
    else 
        return false
}

Solution pseudocode: Iterative inorder traversal using stack

boolean isValidBST(TreeNode root) 
{
    if (root == NULL) 
        return true
    Stack<TreeNode> stack
    TreeNode curr = root
    TreeNode prev = NULL
    while (curr != NULL || stack.isEmpty()== false) 
    {
        if (curr != NULL) 
        {
            stack.push(curr)
            curr = curr->left
        }
        else
        {
            curr = stack.pop()
            if(prev != NULL && curr->value < prev->data) 
                return false
            prev = curr
            curr = curr->right
        }
    }
    return true
}

Time and space complexity analysis

We visit each node only once and perform an O(1) operation with each node. So time Complexity = n* O(1) = O(n). Space complexity depends on the depth of the size of the recursion call stack, which is equal to the height of the tree. So space complexity = O(h).

Critical Ideas to think about!

• How can we modify the above solution to work for duplicate values?
• In the 4th approach using recursive inorder traversal, can we think of implementing without using the pointer by reference?
• Can we think of implementing 2nd approach, using pointers by reference instead of passing the value?
• Is there a way to solve this problem using some other approach?

Suggested problems to practice

• Check if the given binary tree is a strict binary tree or not
• Check whether the given binary is perfect or not
• Check if a binary tree is a complete tree or not
• Check if a binary tree is a subtree of another binary subtree
• Check if the given binary tree is Heap or not
• Check if the given binary tree is SumTree or not

Please write in the message below if you have alternative approaches or find an error/bug in the above approaches. Enjoy learning, Enjoy algorithms!