How to Develop Algorithmic Thinking?

Algorithmic thinking has recently become a buzzword among programmers. It is a method for solving problems based on a clear definition of steps: logical and repetitive. This can help us understand various problem-solving strategies.

Let's understand the importance of algorithmic thinking from a simple perspective. If we observe, two key skills are essential for solving coding problems in programming:

1. Thought process and steps to design an efficient solution.
2. Converting the solution approach into the correct code.

Some programmers may struggle with the first skill, which requires algorithmic thinking. On the other hand, during interviews, some employers may be more interested in how a candidate approaches a problem than the actual implementation of the solution. So, demonstrating expertise in algorithmic thinking can be a way to impress a potential employer.

The critical question is: How do we develop algorithmic thinking independently of learning programming? There are several ways to do it! Let's explore.

Developing Algorithmic Thinking via Solving Puzzles

Solving algorithmic puzzles is an enjoyable activity for developing algorithmic thinking and improving our ability to break down complex problems and develop logical solutions. It will help us to approach coding problems more abstractly and analytically.

For example, we can learn several problem-solving strategies using puzzles:

• Decrease and conquer (Josephus problem)
• Divide and conquer (Finding a fake among eight coins)
• Dynamic programming (Egg dropping puzzle)
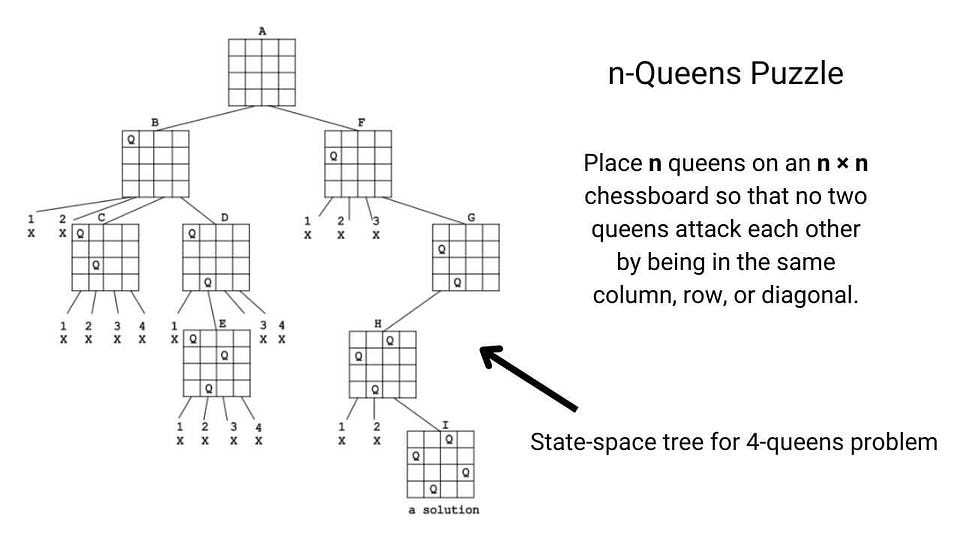
• Backtracking (8-queen puzzle)
• Greedy approach (Fractional knapsack problem)
• String manipulation (Fizz buzz problem)
• Mathematical approach (The water jug puzzle)

Here are some more examples of such types of puzzles:

Puzzle based on the properties of numbers theory

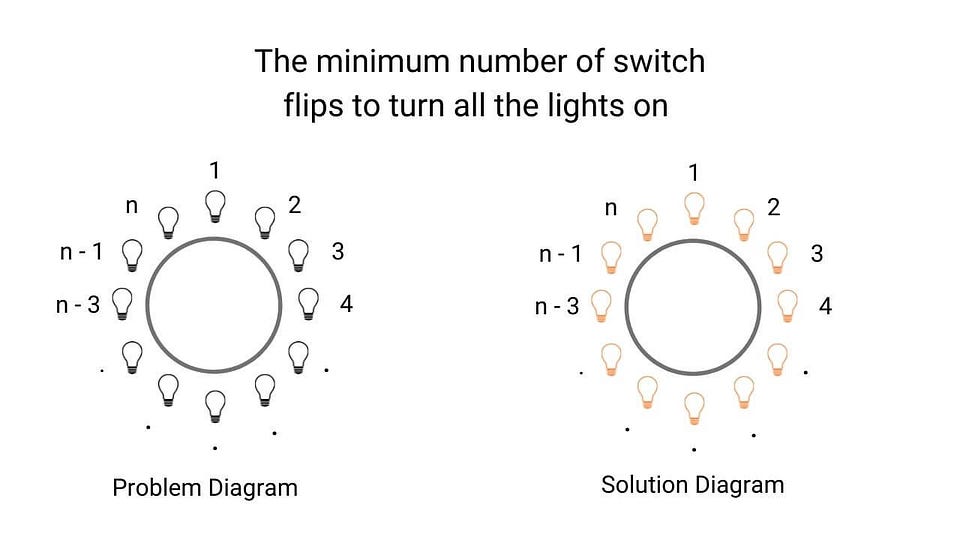
Puzzle based on properties of graph

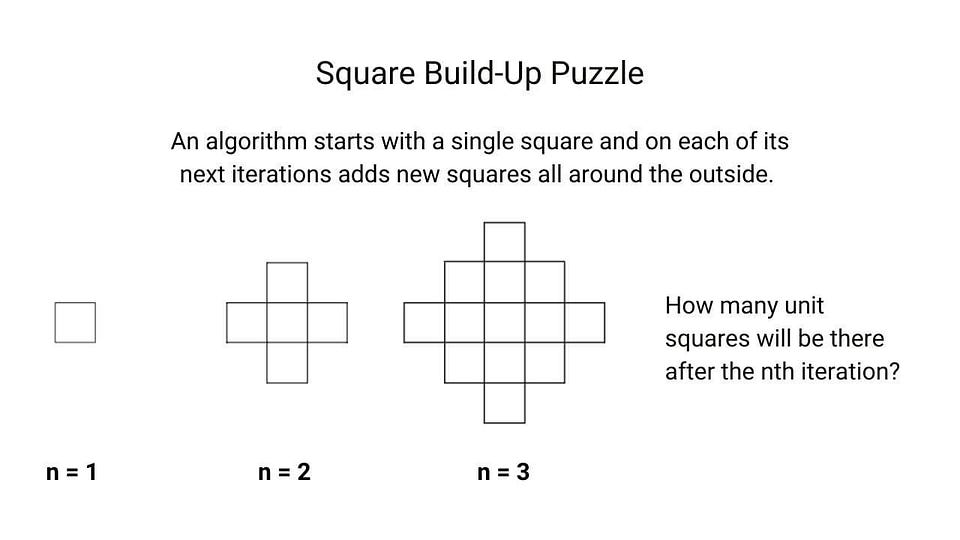
Puzzle based on incremental approach

Puzzle based on graph-based transformation

Puzzle based on dynamic programming

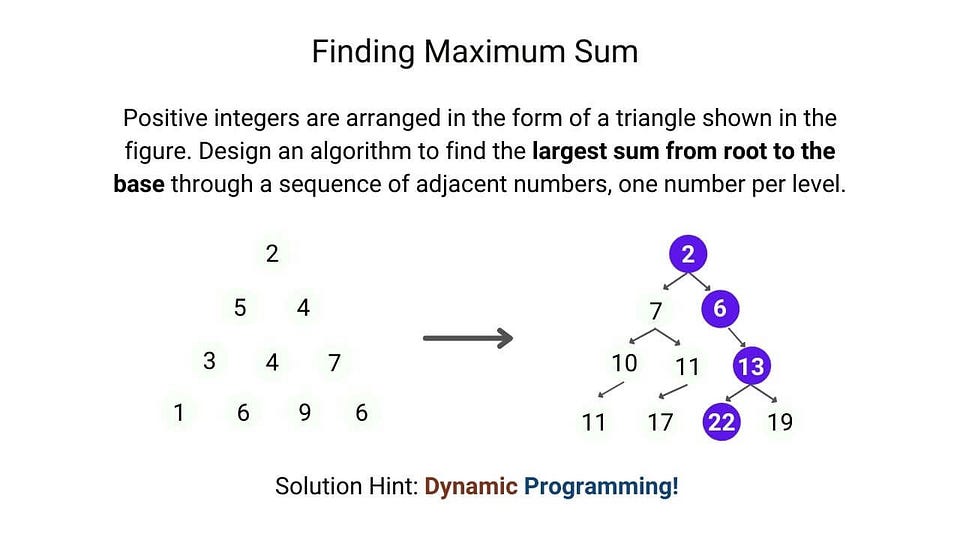
Puzzle based on incremental approach

Puzzle based on idea of backtracking

Puzzle based on iterative elimination

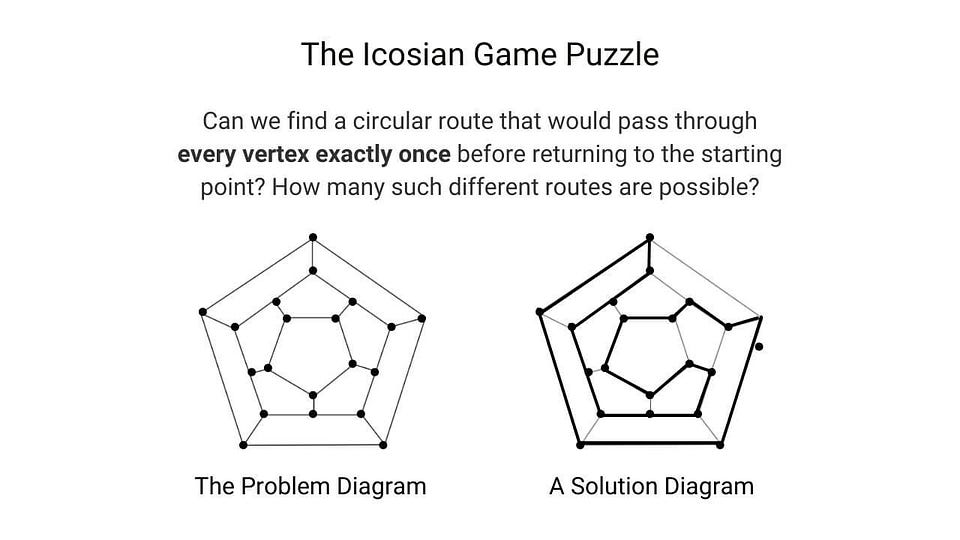
Puzzle based on properties of the graph

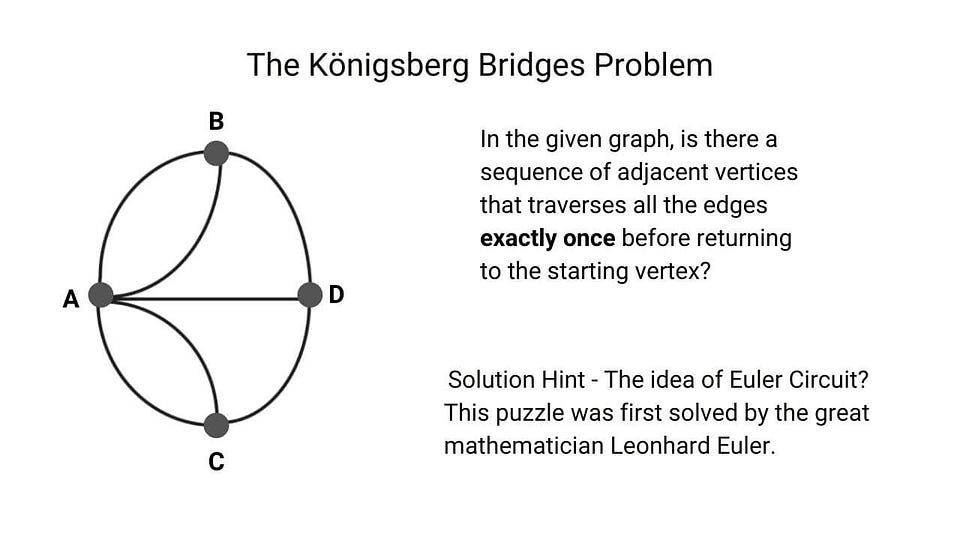
Puzzle based on idea of elimination

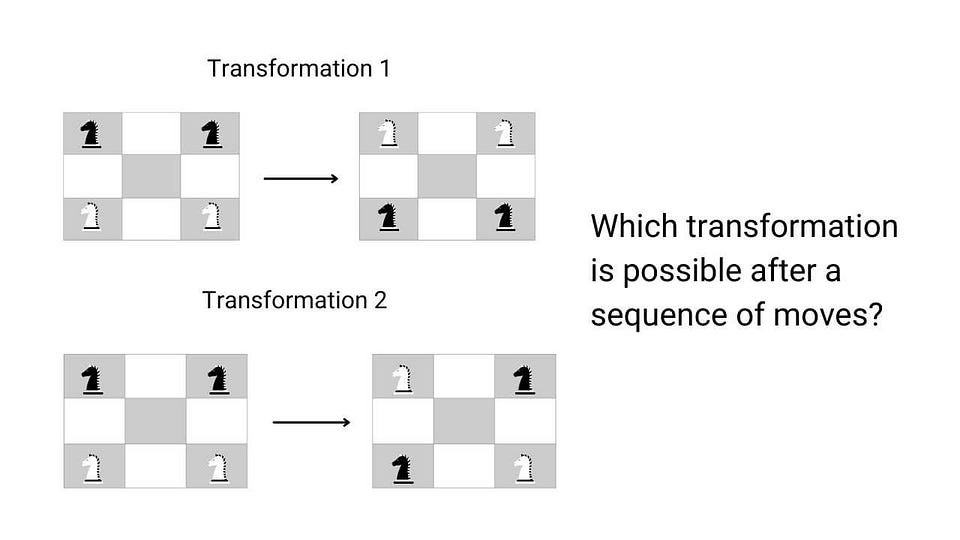
Puzzle based on idea of transformation

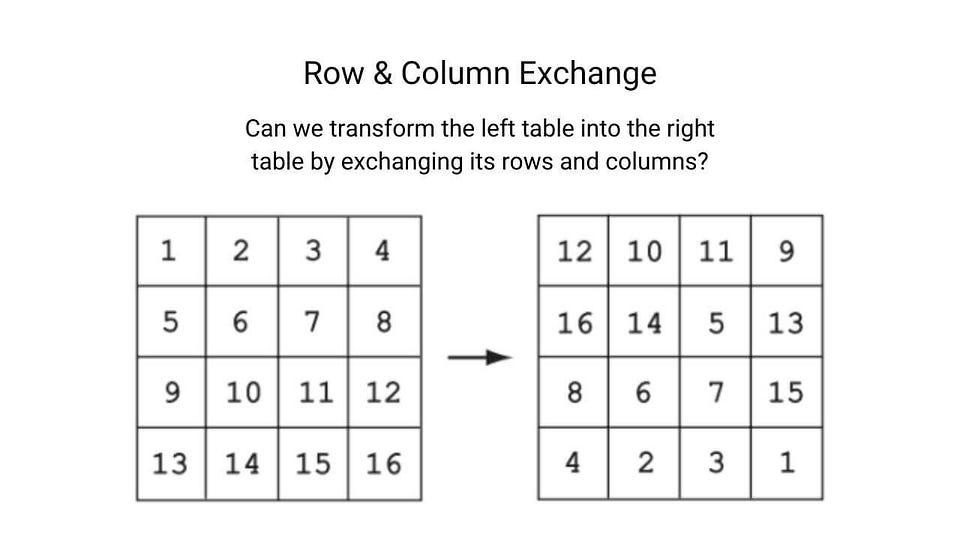
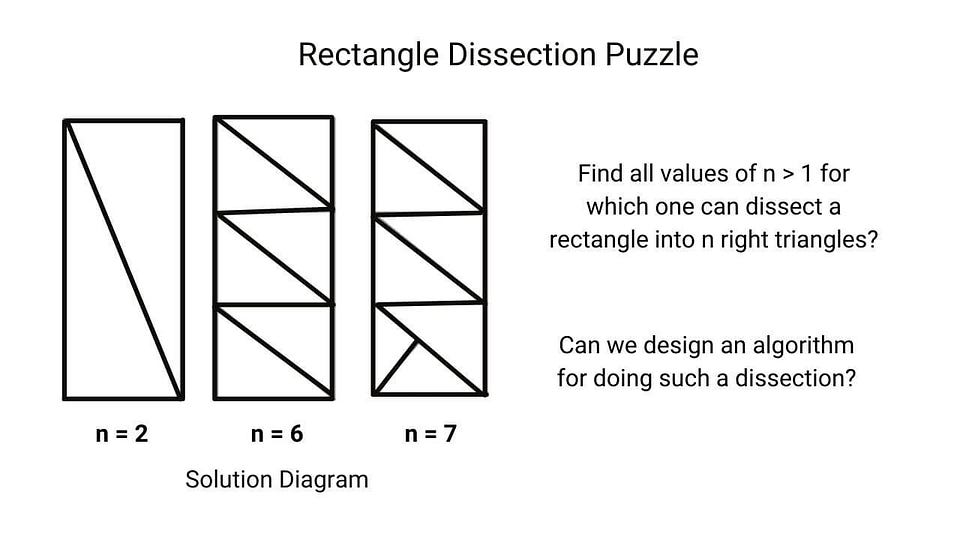
Puzzle based on mathematical counting

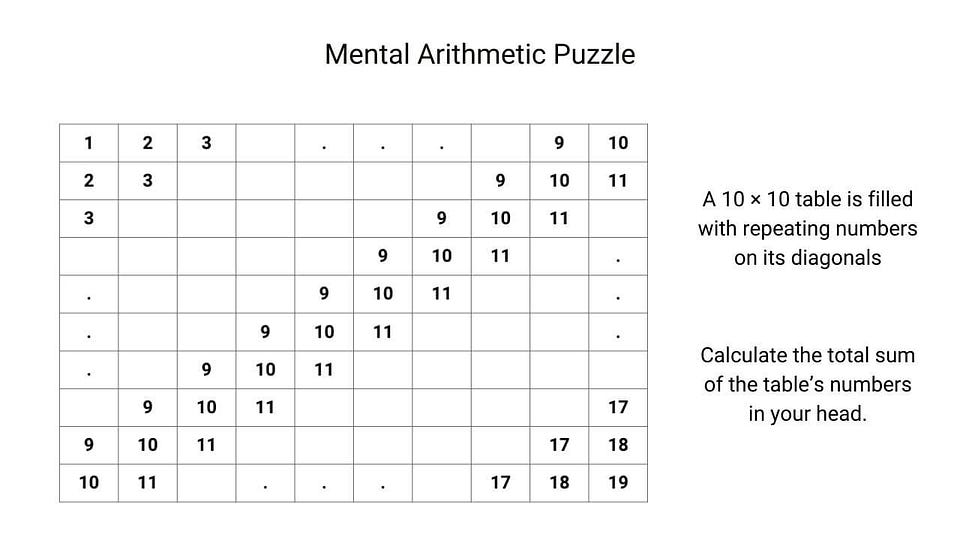
Here are some critical ideas related to solving algorithmic puzzles:

• Every puzzle has an input that defines a specific instance of the puzzle. This input can be either specific (find a fake coin among 8 coins using a balance) or general (find a fake coin among N coins using a balance).
• When working on a specific instance of a puzzle, it's important to focus on the particular instance given to you. This is because other instances of the puzzle may not have the same solution, or may not have a solution at all.
• Even if a puzzle is presented in its general form, it can be helpful to try solving a few small instances first. This can provide valuable insights and help you better understand the solution for the general case.

Developing Algorithmic Thinking via Practicing Steps of Problem-Solving

To solve any problem, it's important to follow a series of well-defined steps. Practising these steps can help us save time, identify patterns that can be applied to multiple coding problems, and effectively find solutions to even the most complex challenges.

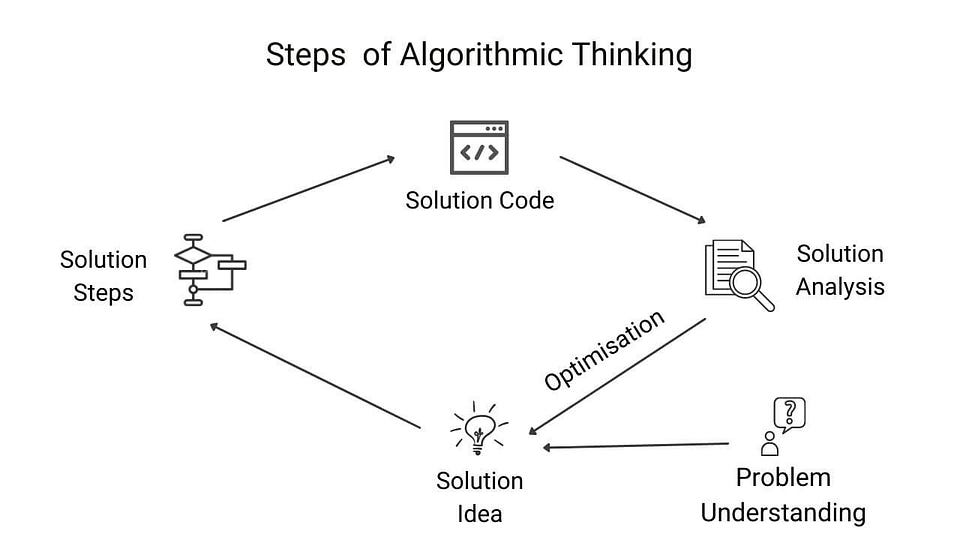
Step 1: Understanding the problem statement

To effectively solve a problem, it's important to clearly understand what is being asked. This involves drawing a visualization of the problem and asking various critical questions.

• Do we understand every word used in the problem?
• What data or information is provided as input?
• What data or results are requested as output?

In addition to this, it's important to understand the computational and non-computational details of the problem like data structures used, input distribution, specific constraints on the input, mathematical properties related to the problem, etc.

Step 2: Selecting concepts and solution strategies

After analyzing the problem description, we need to make predictions about the concepts and approaches necessary to solve it. We can try to think around these questions:

• Will we need to use all of the information provided in the problem?
• Can we eliminate any unnecessary information?
• Which conceptual idea is related to the given problem?
• Which approach would be more appropriate to process the input data and obtain an efficient solution?
• Have we solved any similar problems in the past? If so, how can we use that experience to our advantage?

Identifying concepts and approaches used to solve similar problems can save a lot of time and effort.

Step 3: Formulation of a solution strategy and pseudocode

To design a good solution, it can be helpful to first explore a hand-written approach by going through several examples and developing a general step-by-step strategy. This will involve carefully thinking about each step and identifying common actions for all examples. 

Two types of thinking are important at this stage:

• Iterative thinking: Solving the problem incrementally by building a partial solution.
• Recursive thinking: Solving the problem using smaller sub-problems.

It can be helpful to describe the operations needed to transform the given input into the desired output on paper. From there, you can write out the steps in simple English and translate them into pseudocode or a flowchart. This can help clarify the logic and make it easier to write the final correct code.

Step 4: Correct Programming Implementation

Once you have developed a pseudocode solution, you can move on to implementing it in a programming language such as C++, Java, or Python. During this process, it's important to carefully select programming elements that will help create effective code. This may include elements such as a solution function, helper functions, loops, base cases for recursive code, and variables such as local variables, global variables, and pointers.

It's also important to pay attention to memory management, pre-processing, and other details that can impact the efficiency and correctness of the code. Remember to follow a good coding style to make your code easy to read and understand.

Step 5: Verifying correctness and optimizing further

Once you have implemented your solution, it's important to test it for bugs, analyze its time and space complexity, and think about ways to optimize it further. Here are some ideas that can be helpful:

• Manually trace the input-output pattern by performing a hand trace, or by drawing a plot to describe the behavior of variables or critical steps defined in the solution.
• Identify input cases that cause the algorithm to produce incorrect output. If there is an error or bug, identify and correct the steps responsible for it. Make sure the solution handles all boundary cases.
• Analyze the efficiency of the solution by counting the number of operations with respect to the input size.
• Try to optimize the solution by identifying key details of the problem and attempting a different problem-solving approach. Keep optimizing the solution further until there is no further possibility. Sometimes, it is also possible to optimize the solution code by reducing intermediate steps in the pseudocode.

Here are some popular coding questions to practice the steps of problem-solving. These questions can be solved using four or more approaches.

• Maximum subarray sum problem
• Check for pair in an array with a given sum
• Find the majority element in an array
• Longest common subsequence
• The intersection of two unsorted arrays
• Find the kth largest element in a BST
• The kth smallest element in an array
• Find first missing positive
• Find the maximum difference between two elements
• Trapping rainwater problem
• Minimum number of jumps to reach the end

Algorithmic Thinking via Understanding Real-life Applications

Many applications use efficient strategies to deliver a great user experience and performance. Understanding these strategies is an important step in developing algorithmic thinking. Here are some good examples of these strategies:

• Caching strategies such as LRU (Least Recently Used) and LFU (Least Frequently Used) cache.
• Scheduling strategies such as round-robin scheduling and priority scheduling.
• Hashing strategies can be used for tasks such as hash-based load balancing, data encryption in cryptography, symbol table creation in a compiler, and spelling checks.
• Sorting strategies include comparison-based sorting and linear time sorting.

Enjoy learning, Enjoy thinking!