Segment Tree (Build and Range Query Operations)

What is a Segment Tree?

We use the Segment Tree data structure to efficiently answer multiple range queries on an array. It also allows us to modify the array by replacing an element or an entire range of elements in logarithmic time. In this blog, we will focus on two critical operations: building the segment tree from a given array and performing a range minimum operation on a segment tree.

Let's start with this problem: We have an array with some integers. Now, we receive multiple range queries [l, r], and the answer to each query is the minimum value from the array between the positions l and r.

Example

Suppose the input array is arr[] = [3, 6, 2, 1, 5, 10, 2, 11, 4, 8]. The following are the queries and their corresponding answers.

Range: [4, 8], Output: 2, Explanation: We need to return the minimum value from the array between indices l = 4 and r = 8. So, if we look at the subarray arr[4:8] = [5, 10, 2, 11, 4], the minimum value in this range is 2. So the answer to this query is 2.

Range: [1, 3], Output: 1, Explanation: Similarly, for this query, we return the minimum value from the subarray arr[1:3] = [6, 2, 1], which is 1.

Brute force solution for Range Minimum Query problem

The brute force method to solve this problem is straightforward. We iterate from index l to r in the array for each query, finding the minimum value within this range. Consequently, one query takes O(r - l) time or O(n) time in the worst case. If there are q queries, this method will take O(q * n) time in the worst case. One key insight is clear: as the number of queries increases, our code will take a significant amount of time to process all queries. So, our goal is to design a data structure that can answer each query in O(log n) time.

How does Segment Tree works?

A segment tree is a binary tree in which each node stores information about a specific range, and the nature of that information depends on the problem. In our case, each node will store the minimum value within an interval. However, segment trees can also be used to store various types of information, such as range maximum, range sum, range XOR, and more.

To build a segment tree, we use the array representation of a binary tree. If we follow 0-based indexing, for any node at index i, its children will be found at indices 2i + 1 and 2i + 2. Similarly, with 1-based indexing, the children of a node at index i will be present at indices 2i and 2i + 1. In this blog, we will follow 0-based indexing.

Suppose we are given an array arr[] with a size of n and the segment tree st[].

The root of the segment tree represents the entire range of the array from 0 to n - 1, i.e., arr[0: n-1].
Leaf nodes of st[] represent individual elements from arr[i].
Internal nodes represent an interval arr[i: j], where 0 <= i < j < n.

We then break down this interval into two half intervals. The children of the root node represent the intervals arr[0, n/2] and arr[n/2 + 1, n - 1]. Each interval is further divided into two halves, and the two children of each node represent these halves. Since the segment tree halves in each step, the height of the segment tree is O(log n), and the tree has n leaves, corresponding to the n indices in the array.

For example, explore the following image of the segment tree for the given array. The red text represents the current node's range, the blue text denotes the node's indexes, and the black text shows the minimum value from the array in this range.

Segment tree visualization

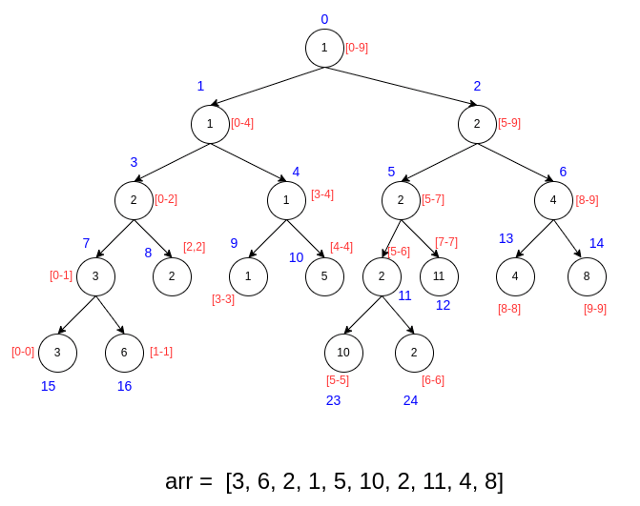
How to Build a Segment Tree for Range Minimum Queries?

Divide and Conquer Idea to Build Segment Tree

As we know, both children of a node share the range of the node equally. Therefore, we can employ a divide-and-conquer strategy to build the segment tree. During the divide step, we proceed top-down and recursively divide the range into two halves until there is only one element left in the range. In this case, the answer is simply that single element.

The formation of the segment tree occurs during the conquer and combine step, which proceeds in a bottom-up fashion, starting from the leaf nodes and moving towards the root node. In other words, it updates the nodes in the path from a leaf to the root in this process, utilizing data from the child nodes to construct a parent node at each step. This recursive process ultimately reaches the root node, which represents the entire array. It's important to note that the combine step may vary for different types of questions, such as range maximum, range sum, and so on.

Divide and Conquer Steps to Build Segment Tree

We define a function buildSegTree(int st[], int arr[], int nodeIndex, int leftRange, int rightRange) that takes these values as input parameters:

st[]: Segment tree array.
arr[]: Input array.
nodeIndex: Index of the current node in the segment tree.
leftRange: Left limit of the current segment.
rightRange: Right limit of the current segment.

Initially, nodeIndex = 0(root node), leftRange = 0, and rightRange = n - 1.

Divide Step: By calculating the mid-index, we divide the array into two halves: leftRange to mid and mid + 1 to rightRange, where mid = leftRange + (rightRange - leftRange)/2.

Conquer Step: We recursively call the same function with modified input parameters to build the segment tree for the left and right half of the array i.e. buildSegTree(st, arr, 2 * nodeIndex + 1, leftRange, mid) and buildSegTree(st, arr, 2 * nodeIndex + 2, mid + 1, rightRange).

Combine Step: This is the most crucial step. We use the data of the child nodes to decide what information the parent node stores. In our case, we need to find the range minimum. So we take the minimum of the values stored in the child nodes and keep them in the parent node i.e. st[nodeIndex] = min (st[2 * nodeIndex + 1], st[2 * nodeIndex + 2]). Note: If we need to find the range sum, we will take the sum of the values stored in the child nodes and store it in the parent node.

Base Case: This is the trivial case when leftRange == rightRange, i.e. this represents a single element from the array which is the situation of a leaf node. The segment tree will store this element i.e. if(leftRange == rightRange), st[nodeIndex] = arr[leftRange].

Size of the array used in Segment Tree Construction

As discussed above, we also represent the segment tree as an array, similar to the heap. The difference here is that the heap is a complete binary tree structure, while the segment tree is a full binary tree structure. The idea is simple: We always divide segments into two halves at every level in a segment tree.

Here are the properties of a full binary tree:

Every node has 0 or 2 children, and all levels are filled except the last level.
In a full binary tree with n leaves, there will be n-1 internal nodes. So the total nodes will be 2*n – 1.
Unlike a complete binary tree, the last level in a full binary tree may have gaps between nodes. So there will be some wastage of space in the simple array representation of a full binary tree. We can think to optimize this wastage, but code for segment tree operations becomes more complex.

If the size of the input array n is a power of 2, then the size of the segment tree is 2n - 1, where the number of leaf nodes is n and the number of internal nodes is n - 1. Now, if we increase the input array size by 1, a new level gets added to the tree. So, if n is not a power of 2, we need to go to the next power of 2. In other words, when the array size n is not a power of 2, approximately 2k - 1 nodes are required for the segment tree, where k is the smallest power of 2 greater than n.

For example, take this array and the corresponding segment tree for finding the minimum in a range, where the size of the array varies from 1 to 5. Initially, arr = [1], st = [1], size of the tree = 1.

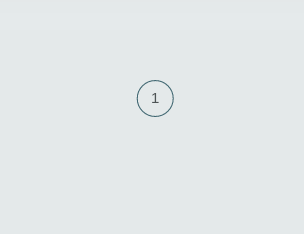
arr = [1, 2], st = [1, 1, 2]

The size of tree = 3 (2n -1, where n = 2).

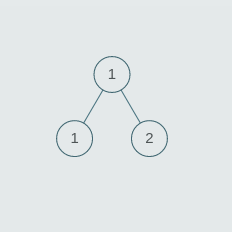
Now n = 3, arr = [1, 2, 3], st =[1, 1, 3, 1, 2, null, null]

Here n is not a power of 2.
The smallest power of 2 greater than n = k = 4.
So the size of the tree = 2 * k - 1 = 2 * 4 - 1 = 7.
If we observe, the height of the tree increases by 1.

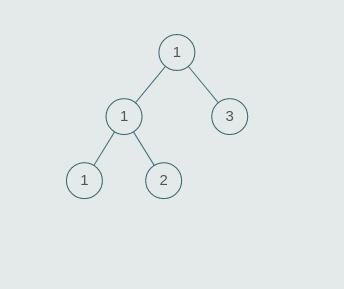
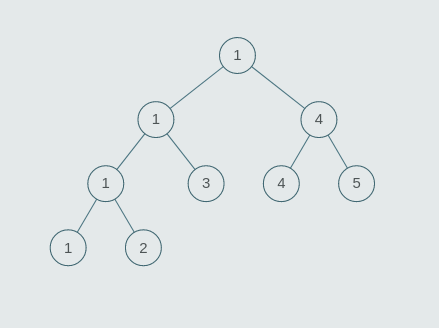
arr = [1, 2, 3, 4], st = [1, 1, 3, 1, 2, 3, 4]

The size of tree = 7 (2n -1, where n = 4).

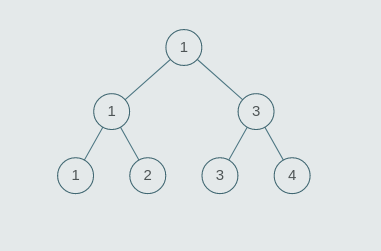
arr = [1, 2, 3, 4, 5], st =[1, 1, 4, 1, 3, 4, 5, 1, 2, null, null, null, null, null, null]

Here n is not a power of 2.
The smallest power of 2 greater than n = k = 8.
So the size of the tree = 2 * k - 1 = 2 * 8 - 1 = 15.
The height of the tree again increases by 1 at this point.

Pseudocode for Building Segment Tree

void buildSegTree(int st[], int arr[], int nodeIndex, int leftRange, int rightRange)
{
    if (leftRange == rightRange)
    {
        // Leaf node
        st[nodeIndex] = arr[leftRange]
    }
    else
    {
        int mid = leftRange + (rightRange - leftRange) / 2
        
        // Recursively building segment tree for left child
        buildSegTree(st, arr, 2 * nodeIndex + 1, leftRange, mid)

        // Recursively building segment tree for right child
        buildSegTree(st, arr, 2 * nodeIndex + 2, mid + 1, rightRange)

        // Union of left and right, which is minimum in our case
        st[nodeIndex] = min(st[2 * nodeIndex + 1], st[2 * nodeIndex + 2])
    }
}

int[] buildSegmentTree(int arr[], int n)
{
    int st[2n - 1]
    for (int i = 0; i < 2n - 1; i = i + 1)
        st[i] = INT_MAX

    buildSegTree(st, arr, 0, 0, n - 1)

    return st
}

Time Complexity of Building a Segment Tree

We recursively solve the problem of size n by solving the two smaller sub-problems of size n/2 and using the solutions of these two smaller problems to answer the parent node.

The time complexity of the divide part is O(1).
The time complexity of the conquer part is 2*T(n/2).
The time complexity of the combine part is O(1).
Thus, overall time complexity T(n) = 2 * T(n/2) + O(1).

We can solve this recurrence using both the recursion tree and the master method. To better understand analysis, you can refer to this blog: Analysis of recursion. If we observe closely, this recurrence relation is similar to the recurrence of the divide and conquer solution of finding max and min in an array. So the time complexity is O(n). In other words, we can build a segment tree in linear time.

Space Complexity of Building a Segment Tree

Space complexity = Space used for st[] array + Space used by recursion call stack.

As discussed above, If the size of the input array n is a power of 2, then the size of the segment tree is 2n -1. If n is not a power of 2, then the segment tree size is 2k - 1, where k is the smallest power of 2 greater than n. So overall, the size of the st[] array will be O(n).
For the recursion call stack, space complexity is O(log n) as the stack frame size depends on the recursion tree's max depth, which is equal to O(log n).

So overall space complexity = O(n) + O(log n) = O(n).

How does Query work in Segment Tree?

Algorithm idea of Range Minimum Query

In this operation, we query on a range and return the answer to the problem (minimum of the range in our case). We start from the root node of the segment tree. At each node, we check for three conditions:

The range represented by the node is completely outside the given range: In this case, we do not move ahead, and we return.
The range represented by a node is entirely inside the given range: In this case, we return the value stored at this node, a minimum of the range defined by the node.
The range represented by a node is partially inside and partially outside the given range: Return the union of the values returned by the left and right nodes depending on the problem statement. We return the minimum of the left and right node values in our case.

Pseudocode of Range Minimum Query

st[]: Segment tree array.
nodeIndex: Index of the current node in the segment tree. This value will be 0 Initially.
leftRange: Left limit of the current node.
rightRange: Right limit of the current node.
l: left limit of the given query.
r: right limit of the given query.

int rangeMinQuery(int st[], int nodeIndex, int leftRange, int rightRange, int l, int r) 
{
    // Case 2: Range represented by node is completely outside the given range
    if (r < leftRange || rightRange < l) 
        return INT_MAX

    // Case 1: Range represented by node is completely inside the given range
    if (l <= leftRange && rightRange <= r)
        
        return st[nodeIndex]

    // Case 3: Range represented by a node is partially inside and partially outside the given range
    int mid = leftRange + (rightRange - leftRange) / 2
    
    int leftMin = rangeMinQuery(st, 2 * nodeIndex + 1, leftRange, mid, l, r)
    int rightMin = rangeMinQuery(st, 2 * nodeIndex + 2, mid + 1, rightRange, l, r)
    
    return min(leftMin, rightMin)
}

Time Complexity of Range Minimum Query

To query a range minimum, we claim that we process at most two nodes at every level. We will attempt to prove this through a contradiction. For example, consider the following tree. Suppose that three nodes are explored at a certain level in the given segment tree.

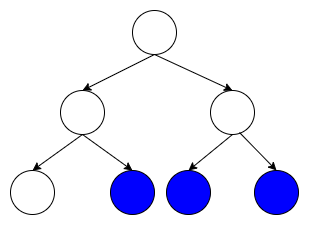
The range covered by these nodes is from the leftmost colored node to the rightmost colored node. However, in this case, the range of the middle node is entirely covered. Thus, this node will immediately return the value and not be explored. Therefore, we proved that we expand at most two nodes at each level, and since there are logn levels, the number of explored nodes is 2logn = O(logn). Thus time complexity of the query operation is O(logn).

Conclusion

In this blog, we studied how to solve multiple queries on an array in logarithmic time. We looked at the build and query operations of the segment tree. In the next blog, we will study the update operation of the segment tree.

Enjoy learning, Enjoy coding, Enjoy algorithms!

Segment Tree Data Structure (Build and Range Query Operations)