Find Maximum and Minimum Element in an Array

Difficulty: Medium, Asked-In: Facebook, Microsoft.

Key Takeaways

• An excellent problem to learn problem-solving using a single loop and divide-and-conquer approach.
• We are incrementing the loop by two to optimize the code. We can use similar ideas to optimize the code for other coding problems.
• Time complexities of all three approaches are O(n), but the total count of comparison operations is different. Such a scenario may arise in solving other coding problems where one can reduce the count of critical operations to optimize the solution.

Let’s understand the problem

Given an array X[] of size n, we need to find the maximum and minimum elements present in the array. Our algorithm should make the minimum number of comparisons.

Examples

Input: X[] = [4, 2, 0, 8, 20, 9, 2], Output: max = 20, min = 0.

Input: X[] = [-8, -3, -10, -32, -1], Output: max = -1, min = -32.

Discussed solution approaches

• Brute force approach using single loop: Increment by 1.
• Using divide and conquer approach similar to merge sort.
• Efficient approach using single loop: Increment by 2.

Brute force solution using single loop: Increment by 1

Solution idea and steps

Step 1: We initialize two variables, max and min, with X[0] to store the maximum and minimum.

Step 2: Now we traverse the array from i = 1 to n - 1 and compare each element with min and max.

• If (X[i] < min): When X[i] is smaller than the minimum so far, we update min with X[i].
• If (X[i] > max): When X[i] is greater than the maximum so far, we update max with X[i].
• By the end of the loop, the minimum and maximum values of the array will be stored in the variables min and max.

Step 3: To return these values, we create an extra array maxMin[] of size two, where we store the maximum at the first index and the minimum at the second index. We return the maxMin array as output.

Solution pseudocode

int[] findMinMax(int X[], int n)
{
    int max = X[0]
    int min = X[0]
      
    for(int i = 1; i < n; i = i + 1)
    {
        if(X[i] > max)
            max = X[i]
        else if(X[i] < min)
            min = X[i]
    }
  
    int maxMin[2] = {max, min}
    return maxMin
}

Solution analysis

We are running a single loop n - 1 time and doing O(1) operations at each iteration. So time complexity = (n - 1)*O(1) = O(n). We are using constant extra space, so space complexity = O(1). The critical questions are: What would be the worst and best-case scenario?

In the worst case, we make two comparisons at each iteration. This occurs if the array is sorted in descending order. In this situation, the first if statement will be false every time, and the second if statement will be true every time. So, the total number of comparisons in the worst case = 2(n−1).

The best case occurs when the elements are sorted in ascending order. In this situation, the first if statement will be true every time, and the second if statement will not execute. So, the total number of comparisons in the best case = n−1.

Using divide and conquer approach similar to merge sort

Solution idea

Now the critical questions are: Can we solve this problem using another approach? Can we think recursively to find maximum and minimum? Let's think!

If we divide the array into two equal parts and find the minimum and maximum of both halves recursively, we can easily find the maximum and minimum of the overall array. For this, we compare the minimum of both halves to get the overall minimum and the maximum of both halves to get the overall maximum. This looks like a divide and conquer idea, similar to the merge sort!

Solution steps

We define function that accepts the array and its start and end indices as input parameters, i.e., findMinMax(int X[], int l, int r).

Base case

If the array size is 1, we return that single element as both the maximum and minimum. On the other hand, we can also consider the base case of an input size of 2 to terminate the recursion earlier. For 2 size array, it will require only one comparison to find the max and min. Note: This will help reduce the number of recursive calls and optimize the code.

The critical question: The base case of size 2 is important but not sufficient. We also need to write the base case for size 1. Why? Here is the reason: We are dividing the array equally. So, in the case of an input size in the 2^k format, like 8 or 16, we will only encounter the size-2 base case. But when the array size is not in the 2^k format, like 9 or 12, we will encounter both base cases of size 1 and size 2. Explore and think!

if(l == r)
{
        max = X[l]
        min = X[l]
}

else if(l + 1 == r)
{
    if(X[l] < X[r])
    {
        max = X[r]
        min = X[l]
    }
    else
    {
        max = X[l]
        min = X[r]
    }
}

Divide: We calculate the mid index i.e. mid = l + (r - l)/2.

Conquer

• We recursively calculate the maximum and minimum for the left part, i.e., leftMinMax[2] = findMinMax(X, l, mid).
• We recursively calculate the maximum and minimum for the right part, i.e., rightMinMax[2] = findMinMax(X, mid + 1, r).

Combine: Now we find the overall maximum and minimum by comparing the min and max of both halves. For this, we need to perform two comparisons only.

if(leftMinMax[0] > rightMinMax[0])
    max = leftMinMax[0]
else
    max = rightMinMax[0]
    
if(leftMinMax[1] < rightMinMax[1])
    min = leftMinMax[1]
else
    min = rightMinMax[1]

Finally, we store max and min in extra memory maxMin[2] and return it.

Solution pseudocode

int[] findMinMax(int X[], int l, int r)
{
    int max, min
    if(l == r)
    {
        max = X[l]
        min = X[l]
    }
    else if(l + 1 == r)
    {
        if(X[l] < X[r])
        {
            max = X[r]
            min = X[l]
        }
        else
        {
            max = X[l]
            min = X[r]
        }
    }
    else
    {
        int mid = l + (r - l)/2
        int leftMinMax[2] = findMinMax(X, l, mid)
        int rightMinMax[2] = findMinMax(X, mid + 1, r)
        if(leftMinMax[0] > rightMinMax[0])
            max = leftMinMax[0]
        else
            max = rightMinMax[0]
        if(leftMinMax[1] < rightMinMax[1])
            min = leftMinMax[1]
        else
            min = rightMinMax[1]
    }
    int maxMin[2] = {max, min}
    return maxMin
}

Solution analysis

This is a recursive solution. So we need to define the recurrence relation to analyze time complexity. Suppose T(n) is the time complexity of problem size n.

• We are dividing problem into two equal size sub-problems of size n/2.
• We are performing 2 comparison operations in the combine step.
• Base case situations occur when n = 2 or n = 1. When n = 2, we are performing 1 comparison operation and when n = 1, we are performing 0 comparison operation.

T(n) = T(n/2) + T(n/2) + 2 = 2T(n/2) + 2, where T(2) = 1 and T(1) = 0.

We can solve this recurrence relation using the recursion tree method or the master theorem. You can explore this blog post: How to analyze recursive functions? Here, we will use the recursion tree method to get the correct insight into the total comparison count. For a better understanding, let's assume that n is a power of 2.

After every level of recursion, the input size of the subproblems decreases by a factor of 1/2. So, the recursion will stop when the input size of the subproblems becomes 2. Let's suppose that after i number of levels, the input size reaches value 2.

=> 2 = n/2^i 
=> 2^(i+1) = n
Taking log both sides 

=> i + 1 = logn 
=> i = logn - 1
So the height of recursion tree = logn - 1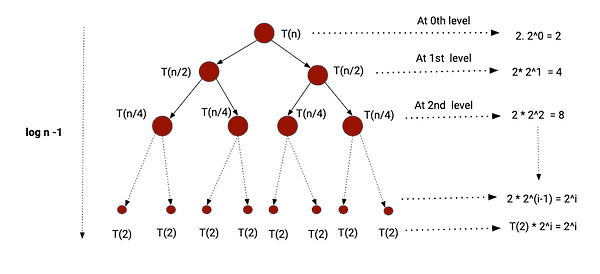

Till (i - 1) level, every subproblem will perform 2 comparisons at the combine step. The last level is the situation of base case, where only one comparison will be made.

• Total comparison count from 0 to (i - 1) level = 2 + 4 + 8 + ... + 2^i = 2 [ 1 + 2 + 4 + ... + 2^(i - 1)] = 2*(2^i - 1). We get this value from the sum of geometric series.
• Total comparison count at i level = 2^i.
• Total count of comparison operations = Total comparison count from 0 to (i - 1) level + Total comparison count at i level = 2*(2^i - 1) + 2^i = 2^(i + 1) + 2^i - 2 = n + n/2 – 2 = 3n/2 – 2.

If n is not a power of 2, it will make more than 3n/2 - 2 comparisons. Overall time complexity = O(n). Here, time complexity is also O(n), but the total count of comparison operation is less than the previous approach.

Space complexity = The size of recursion call stack = The height of recursion tree = O(logn).

Efficient approach  using single loop: Increment by 2

Solution idea

In the first approach, we perform two comparison operations for every element in the worst case. Now the critical question is: can we optimize it further and reduce the total count of comparisons? One idea is to pick elements in pairs and update the minimum and maximum. How? Let's think!

Suppose we have updated the maximum and minimum iteratively in the max and min variables till i-1 index. In the next iteration, we compare a pair of values at i and (i + 1) index.

1. If (X[i] < X[i + 1]): X[i] will be the candidate for the minimum and X[i + 1] will be the candidate for the maximum. So we compare X[i] with min and X[i + 1] with max to update the minimum and maximum, i.e., if (X[i] < min), min = X[i] and if (X[i + 1] > max), max = X[i + 1].
2. If (X[i] > X[i + 1]): Here X[i + 1] will be the candidate for the minimum and X[i] will be the candidate for the maximum, i.e., if (X[i] > max), max = X[i] and if (X[i + 1] < min), min = X[i + 1].

In both scenarios, we will do three comparisons in the worst case to update the maximum and minimum of two elements together. In other words, we save one comparison compared to the first approach where we need four comparisons for two elements in the worst case.

Solution steps

Step 1: Declare the max and min variables. We are exploring 2 elements together, so we need to consider the initialization of variables for both odd and even input sizes. If the array size is odd, we initialize the first element as both min and max. Otherwise, we compare the first two elements and set min to the smaller value and max to the larger value.

if(n % 2 != 0)
{
    max = X[0]
    min = X[0]
    i = 1
}
else
{
    if(X[0] < X[1])
    {
        max = X[1]
        min = X[0]
    }
    else
    {
        max = X[0]
        min = X[1]
    }
    i = 2
}

Step 2: Now we traverse the array and pick elements in pairs. For each pair (X[i], X[i + 1]), we compare both elements. Based on the comparison, we update the max and min variables.

while(i < n)
{
    if(X[i] < X[i + 1])
    {
        if(X[i] < min)
            min = X[i]
        if(X[i + 1] > max)
            max = X[i + 1]
    }
    else
    {
        if(X[i] > max)
            max = X[i]
        if(X[i + 1] < min)
            min = X[i + 1] 
    }
    i = i + 2
}

Step 3: Finally, we store max and min in an extra memory maxMin[2] and return it.

Solution pseudocode

int[] findMinMax(int X[], int n)
{
    int max, min, i
    if(n % 2 != 0)
    {
        max = X[0]
        min = X[0]
        i = 1
    }
    else
    {
        if(X[0] < X[1])
        {
            max = X[1]
            min = X[0]
        }
        else
        {
            max = X[0]
            min = X[1]
        }
        i = 2
    }
    while(i < n)
    {
        if(X[i] < X[i + 1])
        {
            if(X[i] < min)
                min = X[i]
            if(X[i + 1] > max)
                max = X[i + 1]
        }
        else
        {
            if(X[i] > max)
                max = X[i]
            if(X[i + 1] < min)
                min = X[i + 1] 
        }
        i = i + 2
    }
    int maxMin[2] = {max, min}
    return maxMin
}

Solution analysis

For each pair, we perform three comparisons: first between the elements of the pair, and the other two with min and max. The total number of comparisons is 3 * (n-1) / 2 (if n is odd) or 3n/2 – 2 (if n is even). So, the time complexity is O(n). We are using constant extra space, so the space complexity is O(1).

We observe that the total number of comparisons is less than in the first approach. In other words, comparing in pairs helps us optimize the first approach further.

Critical ideas to think!

• Why does incrementing the loop by two help reduce the comparison count?
• How do we modify the above solutions when there are repeated input values?
• Is there any other way to solve this problem?
• In which scenario is the number of comparisons equal for approaches 2 and 3?
• Why is the space complexity O(logn) in the divide and conquer solution? Why are there two base cases? What would be the time complexity if we remove the base case with an array size of 2?
• What would be the best and worst case in the brute force approach?

Comparisons of time and space complexities

• Brute force approach using a single loop: Time complexity = O(n), Space complexity = O(1), Total comparison count in the worst case = 2(n-1).
• Using divide and conquer: Time complexity = O(n), Space complexity = O(logn), Total comparison count = 3n/2 - 2 (If n is a power of 2).
• Efficient approach using a single loop: Time complexity = O(n), Space complexity = O(1), Total comparison count in the worst case = 3n/2 - 2.

Similar coding questions to practice

• Sort an array in the waveform
• Find Majority Element in Array
• Find Maximum Subarray Sum
• Find Maximum Difference in Array
• Finding the maximum and minimum element in a matrix.
• Finding the largest and smallest element in a binary search tree.
• Finding the maximum and minimum element in a rotated sorted array.
• Finding the maximum and second maximum element in an array.

If you have any queries or feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!