Bubble Sort, Selection Sort and Insertion Sort Algorithm

This blog discusses the design, implementation, and time complexity analysis of bubble, selection, and insertion sort algorithms. These are some of the fundamental sorting algorithms to learn problem-solving using an incremental approach.

Input: An array X[] of n integers.

Output: A permutation of the input such that X[0] <= X[1] <= X[2] .... <= X[n-2] <= X[n-1].

Bubble sort algorithm

Bubble sort is a simple and inefficient sorting algorithm. It is generally one of the basic algorithms taught in programming to develop intuition about the working of algorithms. Sometimes bubble sort is also referred to as "Sinking sort"!

How does bubble sort work?

If we look at the elements in the sorted array, the largest element is at the (n - 1)th index, the 2nd largest is at the (n - 2)th index, and so on. So one basic idea would be to traverse the array and place the largest element at the (n - 1)th index. Again, traverse the array and place the second-largest element at the (n - 2)th index, and so on.

• After the 1st iteration, the largest element bubbles up towards the (n - 1)th index. Similarly, after the 2nd iteration, the 2nd largest element bubbles up towards the (n - 2)th index. And so on!
• In general, at any ith iteration, we place the ith maximum element at the (n - i)th index. This process will go on until the whole array becomes sorted.

Bubble sort implementation steps

We will run two nested loops:

• At each stage of the outer loop, we will place one input value to its correct position in the sorted output. So, the outer loop will run n times from i = 0 to n - 1.
• After the ith iteration of the outer loop, i maximum elements will get placed from index (n - i) to (n - 1). At the (i + 1)th iteration, we place the (i + 1)th maximum element at the (n - i - 1)th index. So, we need to run an inner loop from n - i - 1 times.

for (int i = 0; i < n; i = i + 1)
{   
    for (int j = 0; j < n - i - 1; j = j + 1)
    {
         ........
    }
}

The critical question now is: What would be the logic inside the inner loop? The idea would be to start from the first index, compare adjacent pairs of elements from j = 0 to n - i - 2, and swap their positions if they exist in the wrong order. In other words, at each step of the inner loop, if X[j] > X[j + 1], we swap X[j] and X[j + 1].

for (int j = 0; j < n - i - 1; j = j + 1)
{
    if (X[j] > X[j + 1])
    {
        temp = A[j]
        X[j] = X[j + 1]
        X[j + 1] = temp
    } 
}

Bubble sort C++ implementation

void bubbleSort(int X[], int n)
{
    for (int i = 0; i < n; i = i + 1)
    {   
        for (int j = 0; j < n - i - 1; j = j + 1)
        {
            if (X[j] > X[j + 1])
            {
                int temp = X[j];
                X[j] = X[j + 1];
                X[j + 1] = temp;
            } 
        }
    }
}

Critical question: Does this algorithm work perfect if we run the outer loop n - 1 time, i.e. from i = 0 to n - 2? Think!

Bubble sort Python implementation

def bubble_sort(X, n):
    for i in range(n):
        for j in range(n - i - 1):
            if X[j] > X[j + 1]:
                temp = X[j]
                X[j] = X[j + 1]
                X[j + 1] = temp

Bubble sort visualisation

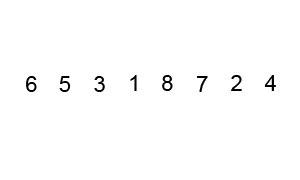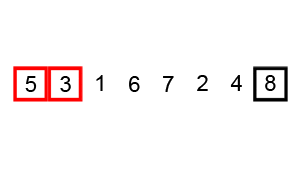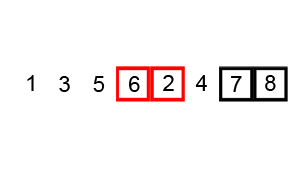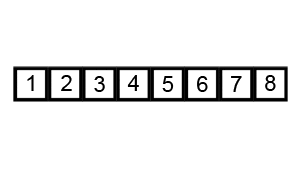
Bubble sort time complexity analysis

We run two nested loops where comparison and swapping are key operations. Regardless of the input, comparison operations will execute every time. On another side, swapping depend upon the order of input, i.e., swapping happens only when comparison X[j] > X[j + 1] is true. So comparison would be the critical operation that decides time complexity in the worst case.

At ith iteration of outer loop, inner loop will run (n - i - 1) times. So total count of nested loop iterations = Sum of (n - i - 1) from i = 0 to n - 1 = (n - 1) + (n - 2) + . . . + 2 + 1 = n(n - 1)/2 = O(n^2)

Bubble sort worst case time complexity

When input is sorted in decreasing order, comparison X[j] > X[j + 1] becomes true for each iteration of the inner loop, and swapping operation will execute every time. So, reverse sorted array will be the scenario of worst-case input in bubble sort.

• Total count of comparison operations = Total count of nested loop iterations = O(n^2)
• Total count of swapping operations = Total count of comparison operations = O(n^2)
• Time complexity of bubble sort in the worst case = O(n^2) + O(n^2) = O(n^2)

Bubble sort best case time complexity

When input is already sorted in increasing order, then comparison X[j] > X[j + 1] becomes false for each iteration of the inner loop, and swapping operation will not execute at all. So, sorted array is the scenario of best case input in bubble sort.

• Total count of comparison operations = Total count of nested loop iterations = O(n^2)
• Total count of swapping operations = 0
• Time complexity of bubble sort in the best case = O(n^2)

In both worst and best cases, bubble sort runs in O(n^2) time complexity. We use constant extra space, so space complexity of bubble sort = O(1).

Optimized implementation of bubble sort

Even if the array is sorted, the above algorithm always works in O(n^2) time. From another perspective, if the array gets sorted in the middle of the nested loop, there is no mechanism to stop the loop, and the loop will continue to run unnecessarily. We can use this insight to optimize bubble sort further. The idea would be to stop the algorithm if the inner loop didn't cause any swaps! The critical question is: How do we do it? Let's think!

If no element gets swapped inside the inner loop, it means the array is finally sorted, and we should stop the bubble sort algorithm. We can detect such a scenario using a boolean variable.

• Before starting the inner loop, we declare a flag, elementSwapped, equal to false.
• When any swap happens inside the inner loop, we set elementSwapped to true.
• By the end of the inner loop, if elementSwapped is still false, it means no swap happened inside the inner loop, and the given array is already sorted. So, we stop the sorting process by breaking the loop. Otherwise, if elementSwapped is true, we should go to the next iteration of the outer loop.

Optimized bubble sort C++ implementation

void optimizedBubbleSort(int X[], int n)
{
    bool elementSwapped;
    for (int i = 0; i < n; i = i + 1)
    {   
        elementSwapped = false;
        for (int j = 0; j < n - i - 1; j = j + 1)
        {
            if (X[j] > X[j + 1])
            {
                int temp = X[j];
                X[j] = X[j + 1];
                X[j + 1] = temp;
                elementSwapped = true;
            } 
        }
        if (elementSwapped == false)
            break;
    }
}

Python implementation

def optimized_bubble_sort(X, n):
    element_swapped = True
    for i in range(n):
        element_swapped = False
        for j in range(n - i - 1):
            if X[j] > X[j + 1]:
                temp = X[j]
                X[j] = X[j + 1]
                X[j + 1] = temp
                element_swapped = True
        if not element_swapped:
            break

In the above implementation, if the array is already sorted, bubble sort makes no swaps, and the algorithm will terminate after a single pass. So, O(n) is the best-case running time for the optimized version of bubble sort. But there is no improvement in the worst-case time complexity, which is still O(n^2) for a reverse sorted array.

Critical ideas to consider in bubble sort

• What would be the average case time complexity of bubble sort?
• What is the idea of "stability" in the case of sorting algorithms? Is bubble sort a stable sorting algorithm?
• Can we modify the above pseudo-code to sort elements in decreasing order?
• Can we think of implementing bubble sort recursively?
• How can we sort linked lists and strings using the bubble sort algorithm?

Selection sort algorithm

How does selection sort work?

The idea of selection sort is simple: We traverse the whole array to find the smallest element. Once we find it, we swap the smallest element with the first element of the array. Then we again look for the smallest element in the remaining array (excluding the first element) and swap it with the second element. This process goes on until the whole array gets sorted.

Selection sort implementation steps

We run two nested loops: The outer loop from i = 0 to n - 2 and the inner loop from j = i to n - 1. In other words, at each iteration of the outer loop, we run the inner loop to find the index of the smallest element in the unsorted subarray and swap it with the value at index i.

So the selection algorithm maintains two subarrays at the ith iteration of the outer loop:

• The sorted subarray X[0…i - 1].
• The unsorted subarray X[i…n - 1].

We build the partially sorted array incrementally by finding the minimum value from the unsorted part and adding it to the sorted part. At each step of the iteration, the sorted subarray size will grow by 1, and the unsorted subarray size will decrease by 1.

Selection sort C++ implementation

void selectionSort(int X[], int n)
{ 
    for (int i = 0; i < n - 1; i = i + 1)
    {
        int minIndex = i;
        for (int j = i; j < n; j = j + 1)
        {
            if (X[j] < X[minIndex])
                minIndex = j;
        }
        swap(X[minIndex], X[i]);
    }
}

Selection sort Python implementation

def selection_sort(X, n):
    for i in range(n - 1):
        min_index = i
        for j in range(i, n):
            if X[j] < X[min_index]:
                min_index = j
        X[i], X[min_index] = X[min_index], X[i]

Selection sort visualisation

Selection sort time complexity analysis

We run two nested loops where the comparison, swapping, and updating of minIndex are key operations. Regardless of the input, comparison and swapping operations will execute every time, but updating minIndex depends on the order of input values.

At the ith iteration of the outer loop, the inner loop will run (n - i) times. So the total count of nested loop iterations = Sum of (n - i) from i = 0 to n - 1 = n + (n - 1) + (n - 2) + . . . + 2 + 1 = n(n + 1)/2 = O(n^2).

Selection sort worst-case time complexity

When the input is sorted in decreasing order, the comparison X[j] < X[minIndex] becomes true every time, and the value of minIndex will get updated every time. So the reverse-sorted array is a worst-case input for selection sort.

• The count of comparison operations = Total count of nested loop iterations = O(n^2).
• We perform one swap on each iteration of the outer loop. The total count of swapping operations = n * O(1) = O(n).
• The total update operation of minIndex = Total count of loop operations = O(n^2).
• The time complexity of selection sort in the worst case = O(n^2) + O(n) + O(n^2) = O(n^2).

Selection sort best-case time complexity

When the input is already sorted, the comparison X[j] < X[minIndex] becomes false every time, and the value of minIndex will not get updated. Therefore, the sorted array is the best-case input for the selection sort.

• The count of comparison operations = Count of nested loop iterations = O(n^2).
• The total count of swap operations = O(n).
• The total update operation of minIndex = O(1).
• The time complexity of selection sort in the best case = O(n^2) + O(n) + O(1) = O(n^2).

So in both worst and best cases, selection sort works in O(n^2) time complexity. We use constant extra space, so the space complexity is O(1).

Critical ideas to think in selection sort

• What is the average case time complexity of the selection sort?
• Is selection sort a stable sorting algorithm?
• The above pseudo-code sorts the array in increasing order. How would you modify the above pseudocode to sort elements in decreasing order?
• How do we implement selection sort recursively?
• How can we use selection sort to sort linked lists and strings?

Insertion sort algorithm

How does insertion sort work?

Insertion sort works much like sorting a hand of playing cards. We begin with an empty left hand and all remaining cards on the table. We remove one card at a time from the table (unsorted array) and insert it into the correct position in the left hand (sorted array). To find the correct place for the card, we compare it with each card already in hand, from right to left.

The core idea is that if the first few elements of an array are sorted, we can easily insert a new element into its correct position in the sorted part. We compare the new element with each element in the sorted part from right to left.

To implement insertion sort, we run two nested loops: an outer loop from i = 1 to n - 1 to pick element X[i], and an inner loop from j = i - 1 to 0 to find the index to insert X[i] in the partially sorted array X[0…i - 1]. During this process, we move elements greater than X[i] to one position ahead of their current position. It's worth noting that we start from i = 1 because i = 0 is a case of a single element that is already sorted.

In general, insertion sort maintains two subarrays at the ith iteration of the outer loop: a sorted subarray X[0…i - 1] and an unsorted subarray X[i…n - 1]. We incrementally build the partial solution by choosing the first value X[i] from the unsorted part and inserting it into the sorted part X[0…i - 1]. In other words, the size of the sorted subarray at each iteration of the outer loop will increase by 1, and the size of the unsorted subarray will decrease by 1.

Insertion sort implementation steps

We run an outer loop from i = 1 to n - 1. At each step of the outer loop:

• We store X[i] in a variable currValue.
• Now we run an inner loop from j = i - 1 to find the correct index to insert currValue in the partially sorted array X[0…i - 1]. For this, whenever X[j] > currValue, we shift X[j] to the right at index j + 1 and decrement j by 1. In simple words, the inner loop will run until j >= 0 and X[j] > currValue.

int currValue = X[i]
int j = i - 1
while (j >= 0 && X[j] > currValue) 
{  
    X[j + 1] = X[j]
    j = j - 1
}

• Whenever the inner loop exits due to the condition X[j] < currValue or j < 0, (j + 1) will be the correct position of currValue. So we insert currValue at the (j + 1)th index, i.e. X[j + 1] = currValue.
• Now we move to the next iteration of the outer loop and continue a similar process to insert remaining elements from the unsorted part into the partially sorted part. After completing the outer loop, X[] contains the sorted output.

Insertion sort C++ implementation

void insertionSort(int X[], int n)  
{  
    for (int i = 1; i < n; i = i + 1) 
    {  
        int currValue = X[i];
        int j = i - 1;  
        while (j >= 0 && X[j] > currValue) 
        {  
            X[j + 1] = X[j];
            j = j - 1; 
        }
        X[j + 1] = currValue;
    }  
}

Insertion sort python implementation

def insertion_sort(X, n):
    for i in range(1, n):
        curr_value = X[i]
        j = i - 1
        while j >= 0 and X[j] > curr_value:
            X[j + 1] = X[j]
            j = j - 1
        X[j + 1] = curr_value

Insertion sort visualization

Image source : CLRS

Insertion sort time complexity analysis

We are running two nested loops where comparison and shifting are critical operations. Regardless of the input, the outer loop will run n - 1 time. But the inner loop's iteration count depends on the comparison X[j] > currValue. So the critical question is: What would be the worst and best-case scenario? Let's think!

Insertion sort worst-case time complexity

This is the situation of a reverse-sorted array, where the outer loop will run n - 1 time, and at each ith iteration of the outer loop, the inner loop will run i times. Why? Because the condition X[j] > currValue will be true for every value from j = i - 1 to 0. In another way: To insert the ith value in its correct position, we shift all values from j = i - 1 to 0 to one right.

So at the ith iteration of the outer loop: Count of comparison operations = i and Count of shifting operations = i

• Total comparison operations = 1 + 2 + 3 + ….+ n - 2 + n - 1 = n(n - 1)/2 = O(n²).
• Total shifting operations = 1 + 2 + 3 + ….+ n - 2 + n - 1 = n(n - 1)/2 = O(n²).
• So the worst-case time complexity of insertion sort = O(n²) + O(n²) = O(n²).

Insertion sort best-case time complexity

This is the situation of a sorted array, where the outer loop will run n - 1 time, and the inner loop will run only once. Why? Because every time we enter into the inner loop, the condition X[j] > currValue will be false, and we exit the inner loop. In another way: the ith value is already at the correct position. So we need to perform only one comparison at each iteration of the outer loop.

• Total comparison operations = n - 1 = O(n).
• Total shifting operations = 0 = O(1).
• So the best-case time complexity of insertion sort = O(n) + O(1) = O(n).

Critical ideas to think in insertion sort

• Due to the best-case scenario, insertion sort is one of the fastest sorting algorithms for partially or almost sorted arrays, i.e., the time complexity is O(kn), where each element is no more than k places away from its sorted position.
• Insertion sort is one of the fastest sorting algorithms for small input sizes.
• Insertion sort is a stable sorting algorithm.
• We can optimize insertion sort further using binary search.
• Insertion sort is a more efficient sorting algorithm than selection and bubble sort.
• The average case time complexity of the insertion sort is closer to the worst-case time complexity, i.e. O(n²).
• The above pseudo-code sort the array in increasing order. How do we modify the above pseudo-code to sort the elements in decreasing order?
• How can we implement the Insertion sort recursively?
• How can we sort linked lists and strings using selection sort?

Comparison of bubble sort vs selection sort vs insertion sort

CritIcal concepts to explore further in sorting

• Concept of stability in sorting algorithms
• What is comparison-based sorting? Explore the design, code, and analysis of merge sort, quicksort, heap sort, shell sort, BST sort, etc.
• Comparison of various sorting algorithms
• Linear time sorting algorithms: Counting sort, Radix sort, Bucket sort
• Problem-solving using sorting
• Real-life applications of sorting

Sorting based coding problems to practice

• Sort an array of 0s, 1s, and 2s
• Sort an array in a waveform
• Sort an array according to the order defined by another array
• Sort the even positioned elements in the ascending order and the odd positioned elements in the descending order. 
• Count swaps required to sort an array using insertion sort
• Merge two sorted arrays, find the intersection of two sorted array

Content references

• Algorithms by CLRS
• The Algorithm Design Manual by Steven Skiena

If you have any queries/doubts/feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!