Counting Sort Algorithm

Difficulty: Medium, Asked-in: Microsoft, Amazon

Introduction to linear time sorting

As we know that any sorting algorithm that relies on comparisons between elements (such as merge sort or quicksort) will take at least O(nlogn) time to sort an input. This is known as the lower bound for comparison-based sorting algorithms. But, it's possible to do better than O(nlogn) under certain conditions. For example, if the input is almost sorted, the insertion sort algorithm can sort it in O(n) time. Similarly, if the input only contains 0's, 1's, and 2's, we can sort it in O(n) time.

What is counting sort?

Counting sort is a sorting algorithm that has a time complexity of O(n) under certain conditions. Specifically, if the input elements are integers between 0 and k, the counting sort can sort the input in O(n + k) time. This means that if k is proportional to n (i.e. k = O(n)), this algorithm works in O(n).

This makes the counting sort a useful tool for sorting input with a small range of integer values. However, it's important to note that the counting sort is not a comparison-based sorting algorithm.

How does counting sort work?

Counting sort uses the indices of the array to determine the correct position of each element in the sorted array. To do this, it first counts the number of elements that are less than a given element x. It then places x in its correct position in the sorted array based on this count. For example, if there are 17 elements less than x, then x belongs in the 18th position in the sorted array.

However, if the input array contains repeated elements, the counting sort needs to be modified slightly. When values are repeated, we don't want to place the same elements in the same position in the output. So we need to maintain the stable order of elements, which means that if A[i] == A[j] and i < j, then A[i] should appear before A[j] in the sorted output.

Implementation steps

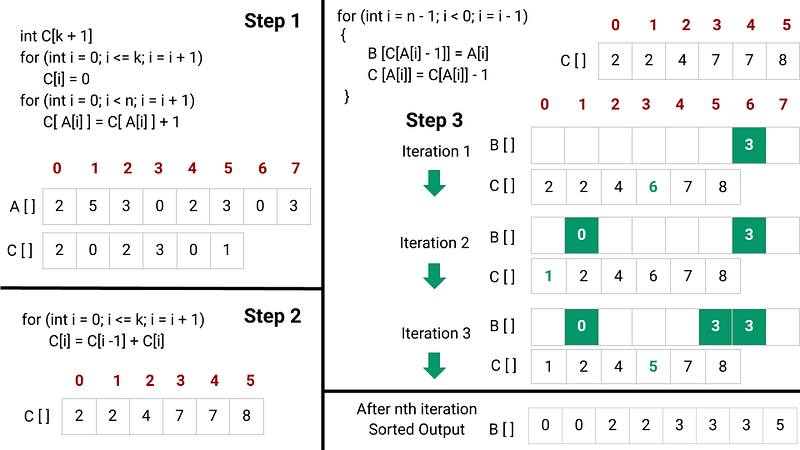
Step 1

The counting sort algorithm uses two additional arrays to help sort the input: an array B[n] to store the sorted output and an array C[k+1] to store the count of every possible unique element in the input.

The size of the count array C[] is k+1 because the range of input values is [0, k]. This means that there are k+1 possible unique elements in the input. By counting the number of occurrences of each unique element in the input and storing them in C[], the counting sort algorithm is able to determine the correct position of each element in the sorted output.

At the start, we initialize all values of C[] to 0's.

for (int i = 0; i <= k; i = i + 1)
    C[i] = 0

Step 2

We first need to count the number of occurrences of each unique element in the input array A[]. To do this, we traverse the input array A[] from the start, using a loop to inspect each element. If we find an element with the value A[i], we increment the count value at C[A[i]].

By the end of this process, the array C[] will hold the count of elements equal to A[i] for each integer 0 <= A[i] <= k. In other words, C[A[i]] will contain the number of times the value A[i] appears in the input array A[].

for (int i = 0; i < n; i = i + 1)
    C[A[i]] = C[A[i]] + 1

Step 3

So at this point, the frequency of each element A[i] is stored in array C[]. To determine the position of each element in the sorted output, we need to modify the array C[] to count the number of elements that are less than or equal to each element A[i].

To do this, we can use the following formula: Number of elements less than or equal to element A[i] = C[0] + C[1] + ... + C[A[i] - 1] + C[A[i]] = Number of elements less than or equal to element (A[i] - 1) + C[A[i]]. This means that we can perform a running sum on the array C[] from i = 0 to k in order to store the count of elements less than or equal to i for all i in one go.

for (int i = 0; i <= k; i = i + 1)
    C[i] = C[i - 1] + C[i]

Step 4

At this point, the array C[] will be in increasing order, with the cumulative sum of all elements less than or equal to A[i] stored at C[A[i]]. To place each element A[i] into its correct position in the output array B[], we traverse the input array A[] from left to right.

If all n elements in A[] are distinct, the correct final index of A[i] in the output array B[] will be C[A[i]] - 1, since there are C[A[i]] elements less than or equal to A[i]. However, if the elements in A[] are not distinct, we need to modify this process slightly to maintain a stable order for repeated elements.

To do this, we traverse A[] from the right end and decrement C[A[i]] each time after placing A[i] into B[]. Decrementing C[A[i]] causes another element with value A[i] to go to the position immediately before the previous A[i] in the output array B[]. In this way, we can ensure that the output array B[] is correctly sorted and stable, even if the input array A[] contains repeated elements.

for (int i = n - 1; i < 0; i = i - 1)
{   
    B[C[A[i]] - 1] = A[i] 
    C[A[i]] = C[A[i]] - 1
}

• By the end of above process, our sorted output will be stored in array B[].

Pseudocode

void countingSort(int A[], int B[], int k, int n)
{
    int C[k + 1] 
    for (int i = 0; i <= k; i = i + 1)
        C[i] = 0
    
    for (int i = 0; i < n; i = i + 1)
        C[A[i]] = C[A[i]] + 1

    for (int i = 0; i <= k; i = i + 1)
        C[i] = C[i - 1] + C[i]

    for (int i = n - 1; i < 0; i = i - 1)
    {   
        B[C[A[i]] - 1] = A[i] 
        C[A[i]] = C[A[i]] - 1
    }
}

Counting sort visualization

C++ Implementation

// Function to sort the array using counting sort
void countingSort(int A[], int B[], int k, int n)
{
    int C[k + 1];

    // initialize count array with zeros
    for (int i = 0; i <= k; i = i + 1)
        C[i] = 0;

    // store the count of each element in the count array
    for (int i = 0; i < n; i = i + 1)
        C[A[i]] = C[A[i]] + 1 ;

    // store the cumulative count of each element in the count array
    for (int i = 1; i <= k; i = i + 1)
        C[i] = C[i] + C[i - 1];

    // place the elements in the sorted array
    for (int i = n - 1; i >= 0; i = i - 1)
    {
        B[C[A[i]] - 1] = A[i];
        C[A[i]] = C[A[i]] - 1;
    }
}

Python implementation

def countingSort(A, B, k, n):
    C = [0] * (k + 1)

    # initialize count array with zeros
    for i in range(k + 1):
        C[i] = 0
    
    # store the count of each element in the count array
    for i in range(n):
        C[A[i]] = C[A[i]] + 1
    
    # store the cumulative count of each element in the count array
    for i in range(1, k + 1):
        C[i] = C[i] + C[i - 1]
    
    # place the elements in the sorted array
    for i in range(n - 1, -1, -1):
        B[C[A[i]] - 1] = A[i]
        C[A[i]] = C[A[i]]- 1

Java implementation

void countingSort(int[] A, int[] B, int k, int n) 
{
    int[] C = new int[k + 1];

    // initialize count array with zeros
    for (int i = 0; i <= k; i = i + 1)
        C[i] = 0;

    // store the count of each element in the count array
    for (int i = 0; i < n; i = i + 1)
        C[A[i]] = C[A[i]] + 1;

    // store the cumulative count of each element in the count array
    for (int i = 1; i <= k; i + 1)
        C[i] = C[i] + C[i - 1];

    // place the elements in the sorted array
    for (int i = n - 1; i >= 0; i = i - 1) 
    {
        B[C[A[i]] - 1] = A[i];
        C[A[i]] = C[A[i]] - 1;
    }
}

Time and space complexity analysis

The counting sort algorithm consists of four loops:

• The first loop takes O(k) time.
• The second loop takes O(n) time.
• The third loop takes O(k) time.
• The fourth loop takes O(n) time.

The overall time complexity of the counting sort = O(k) + O(n) + O(k) + O(n) = O(k + n). If k = O(n), the time complexity of the counting sort algorithm becomes O(n).

The space complexity of the counting sort = Size of the output array B[] + Size of the count array C[] = O(n) + O(k) = O(n + k). If k = O(n), the space complexity of the counting sort becomes O(n).

Properties of counting sort

There are a few important points to consider when using the counting sort algorithm:

• The time and space complexity of counting sort depend on the range of the input data. It works efficiently if the range of the input data is not significantly greater than the number of elements to be sorted. If k = O(n^2), the time and space complexity of counting sort will be O(n^2).
• Counting sort is able to beat the O(nlogn) lower bound of comparison-based sorting algorithms because it does not use comparison operations to sort the input. Instead, it uses the actual values of the elements to determine their correct position in the output.
• The stability property of counting sort is important when additional data are carried around with the elements being sorted. It is also important for another reason: counting sort is often used as a subroutine in the radix sort algorithm, which relies on the stability of counting sort to correctly sort the input.
• Counting sort uses an idea similar to the direct addressing method of hashing.

Critical ideas to think!

There are a few questions to consider when working with the counting sort algorithm:

• How can we extend the counting sort algorithm to work for negative inputs?
• Why do we run the last loop from the right end of the input array A[]?
• Instead of running the last loop from i = n - 1 to 0, could we modify the above implementation by running the loop from i = 0 to n - 1? Would the modified algorithm be stable?
• How do we modify the above algorithm if we want to sort input data given in the range from [a, b]?
• Can you describe an algorithm for the following problem: given n integers in the range 0 to k, preprocess the input and then answer any query about how many n integers fall into a given range [a...b] in O(1) time. The algorithm should use O(n + k) preprocessing time.

Reference: Algorithms by CLRS

Enjoy learning, Enjoy algorithms!