Time Complexity Analysis of Loop in Programming

Loop is a fundamental problem-solving operation in programming, and solutions to many coding problems involve various kinds of loop structures. Even some problem-solving approaches are totally based on a loop:

• Building partial solutions using a single loop and nested loops
• Two-pointers approach
• Sliding window approach
• BFS traversal of graph and tree
• Bottom-up approach of dynamic programming
• Problem-solving using data structures like stack, queue, hash table, heap, etc. 

So the time complexity of such solutions depends on the loop pattern and operations inside the loop. There are two loop patterns that frequently appear in the solution of coding problems:

• Single loop: A loop running constant time, a loop running n times, a loop growing exponentially, a loop running based on a specific condition, a loop running with a data structure, consecutive single loops, etc.
• Nested loops: Two nested loops, three nested loops, a sequence of a single loop followed by nested loops, etc.

One idea is simple: To design a better algorithm or optimize the code further, we should learn to analyze the time complexity of the loop in terms of Big-O notation. Learning the time complexity analysis of loops is not difficult. After practising various loop patterns, we can make optimization decisions quickly and save time.

Steps to analyze the time complexity of loop

Counting total loop iteration in the worst case: we can get this insight by considering the worst-case scenario, initial and final value of the loop variable, loop condition, and increment or decrement operation. Most of the time loop will run for each data element or total input size.

Calculating time complexity of code in the loop body: loop executes this code on each iteration to get the final result. This code may contain conditional statements, comparison operations, swapping operations, assignment operations, etc.

So the time complexity of the loop = (Count of loop iterations in the worst case) * (Time complexity of code in the loop body). We represent this in Big-O notation by ignoring lower-order terms and coefficients.

Sometimes, we can also follow another simple approach:

• Identify the most critical operation inside the loop, which executes the maximum number of times in the worst case. This critical operation would be dominating factor in the time complexity function.
• Now, calculate the total count of this operation for the complete loop in terms of input size. Representing this expression in terms of Big-O notation will give the time complexity of the loop.

Let’s analyze the time complexity of various loop patterns.

Time complexity analysis of single for and while loop

for and while loop running constant times: O(1)

for (int i = 1; i <= c; i = i + 1) 
{  
    Some O(1) expressions
}

// while loop version
int i = 1;
while (i <= c) 
{
    Some O(1) expressions
    i = i + 1;
}

Here loop is running constant times and performing O(1) operation at each iteration. Time complexity = c * O(1) = O(1) * O(1) = O(1).

for and while loop running n times and incrementing/decrementing by constant: O(n)

Example 1: Loop incrementing by some constant c.

for (int i = 1; i <= n; i = i + c) 
{  
    Some O(1) expressions
}

// while loop version
int i = 1;
while (i <= n) 
{
    Some O(1) expressions
    i = i + c;
}

Example 2: Loop decrementing by some constant c.

for (int i = n; i > 0; i = i - c) 
{
    Some O(1) expressions
}

// while loop version
int i = n;
while (i > 0) 
{
    Some O(1) expressions
    i = i - c;
}

Here both loops are running n/c times and performing O(1) operation at each iteration. Time complexity = n/c * O(1) = O(n) * O(1) = O(n).

for and while loop running constant multiple of n: O(n)

for (int i = 1; i <= c*n; i = i + 1) 
{
    Some O(1) expressions
}

// while loop version
int i = 1;
while (i <= c * n) 
{
    Some O(1) expressions
    i = i + 1;
}

Here loop is running cn times and performing O(1) operation at each iteration. Time complexity = cn * O(1) = O(n) * O(1) = O(n).

Two pointers for and while loop: O(n)

l = 0, r = n - 1
while (l <= r) 
{
    if (condition) 
    {
        Some O(1) expressions
        l = l + 1
    }    
    else 
    {
        Some O(1) expressions
        r = r - 1
    }
    Some O(1) expressions
}

// for loop version
for (int l = 0, r = n - 1; l <= r; ) 
{
    if (some condition) 
    {
        Some O(1) expressions
        l = l + 1;
    }
    else 
    {
        Some O(1) expressions
        r = r - 1;
    }
    Some O(1) expressions
}

In the above loop, based on some conditions, we are either incrementing l or decrementing r by 1 and performing O(1) operation at each iteration. Here loop will run n times because l and r are starting from opposite ends and stop when l > r. So time complexity = n * O(1) = O(n).

for and while loop incrementing/decrementing by constant factor: O(logn)

Example 1: Loop incrementing by factor of 2.

for (int i = 1; i < n; i = i*2) 
{
    Some O(1) expressions
}

// while loop version
int i = 1;
while (i < n) 
{
    Some O(1) expressions
    i = i * 2;
}

Example 2: Loop decrementing by factor of 2.

for (int i = n; i > 0; i = i/2) 
{
    some O(1) expressions
}

// while loop version
int i = n;
while (i > 0) 
{
    Some O(1) expressions
    i = i / 2;
}

Here loop is running in the range of 1 to n, and the loop variable increases or decreases by a factor of 2 at each iteration. So, we need to count the total number of iterations performed by the loop to calculate the time complexity.

Let’s assume the loop will terminate after the k steps where the loop variable increases or decreases by a factor of 2. So, 2^k must be equal to the n => 2^k = n => k = logn. So the loop will run logn number of times and do O(1) operation at each step. Time complexity = k * O(1) = logn* O(1) = O(logn).

for and while loop incrementing by some constant power: O(log(logn))

// Here c is a constant greater than 1   
for (int i = 2; i < = n; i = pow(i, c)) 
{ 
    Some O(1) expressions
}

// while loop version
int i = 2;
while (i <= n) 
{
    Some O(1) expressions
    i = pow(i, c);
}

In this case, the loop runs from 1 to n, but the loop variable increases by a factor of i^c. How do we calculate the total number of loop steps? Let's consider the following:

• The first iteration of the loop starts with i = 2.
• In the second iteration, the value of i is 2^c.
• In the third iteration, the value of i is (2^c)^c = 2^(c²).
• This pattern continues until the end. At the ith iteration, the value of i is 2^(c^i).
• The loop will end when 2^(c^i) = n.

2^(c^i) = n
Let's take log of base 2 from both sides.
=> log2(2^(c^i)) = log2(n)
=> c^i = logn

Again take log of base c from both sides.
=> logc(c^i) = logc(logn)
=> i = logc(logn)

So the loop will run log(log(n)) number of times, where each iteration will take O(1) time. So overall time complexity = log(log(n)) * O(1) = O(log(log(n))).

Consecutive single loops: O(m + n)

for (int i = o; i < m; i = i + 1) 
{  
    Some O(1) expressions
}
for (int i = 0; i < n; i = i + 1) 
{
    Some O(1) expressions
}

For calculating such consecutive loops, we do the sum of the time complexities of each loop. So overall time complexity = Time complexity of loop 1 + Time complexity of loop 2 = O(m) + O(n) = O(m + n).

Time complexity analysis of nested for and while loops

The time complexity of nested loops is equal to the number of times the innermost statement is executed.

Two nested for and while loops: O(n²)

for (int i = 0; i < n; i = i + 1) 
{
    for (int j = 0; j < n; j = j + 1) 
    {
          Some O(1) expressions
    }
}

// while loop version
int i = 0;
while (i < n) 
{
    int j = 0;
    while (j < n) 
    {
        Some O(1) expressions
        j = j + 1;
    }
    i = i + 1;
}

In the above nested-loop example, the inner loop is running n times for every iteration of the outer loop. So the total number of nested loop iterations = Total iteration of the outer loop * Total iteration of the inner loop = n * n = n². At each step of the iteration, the nested loop is doing O(1) operation. So overall time complexity of nested for loops = n² * O(1) = O(n²).

for (int i = 0; i < n; i = i + 1) 
{
    for (int j = i + 1; j < n; j = j + 1) 
    {
        Some O(1) expressions
    }
}

// while loop version
int i = 0;
while (i < n) 
{
    int j = i + 1;
    while (j < n) 
    {
        Some O(1) expressions
        j = j + 1;
    }
    i = i + 1;
}

In the above-nested loop example, the outer loop is running n times and for every iteration of the outer loop, the inner loop is running (n - i) times. So total number of nested loop iteration = (n - 1) + (n - 2) + (n - 3)…..+ 2 + 1 = Sum of arithmatic series from (i = 0 to n - 1) = n(n - 1)/2 = n²/2 - n/2 = O(n²). At each step of the iteration, the nested loop is doing O(1) operation. So overall time complexity = O(n²) * O(1) = O(n²). 

Let's take an interesting example of a nested loop. Suppose, we have an input matrix X[ ] of size m x n containing only 0's and 1's, which are sorted in a row-wise fashion. Now here is the loop structure to find the row with a max number of 1s. What will be the time complexity of this loop?

int j = n - 1;
for (int i = 0; i < m; i = i + 1)
{
    while (j >= 0 && X[i][j] == 1)
    {
        j = j - 1;
        // Some O(1) operation
    }
}

There are two nested loops in the code and the time complexity looks O(mn). But this is not the correct analysis. If we observe closely, we traverse each row and column once, i.e. outer loop traverses each row, and the inner loop traverses each column. Think!

So total loop iteration = Total number of rows + Total number of columns = m + n. At each loop iteration, we are doing O(1) operation. So time complexity = Total loop iteration*O(1) = (m + n) * O(1) = O(m + n).

Note: It’s an exercise for you to analyze the following loop.

for (int i = 0; i < n; i = i + 1) 
{
    int j = i
    while (j > 0) 
    {
        Some O(1) expressions
        j = j - 1
    }
}

Combination of single and nested loops

In such a case, we need to do the sum of the time complexities of each loop, but time complexity will be dominated by the time complexity of the nested loop.

for (int i = 0; i < n; i = i + 1) 
{
    Some O(1) expressions
}

for (int i = 0; i < n; i = i + 1) 
{
    for (int j = 0; j < m; j = j + 1) 
    {
        Some O(1) expressions
    }
}

for (int k = 0; k < n; k = k + 1) 
{
    Some O(1) expressions
}

Time complexity = Time complexity of loop 1 + Time complexity of loop 2 + Time complexity of loop 3 = O(n) + O(mn) + O(n) = O(mn).

Three nested for and while loops: O(n³)

for (int i = 0; i < m; i = i + 1) 
{
    for (int j = 0; j < n; j  = j + 1) 
    {
        for (int k = 0; k < n; k  = k + 1)
        {
            Some O(1) expressions
        }    
    }
}

// while loop version
int i = 0;
while (i < m) 
{
    int j = 0;
    while (j < n) 
    {
        int k = 0;
        while (k < n) 
        {
            Some O(1) expressions
            k = k + 1;
        }
        j = j + 1;
    }
    i = i + 1;
}

All three nested loops are running n times and doing O(1) operation at each iteration, so time complexity = n * n * n * O(1) = n³ * O(1) = O(n³) * O(1) = O(n³).

for(int i = 1; i < n; i = i + 1) 
{   
    for(int j = i + 1; j <= n; j  = j + 1) 
    {
        for(k = i; k <= j; k  = k + 1) 
        {
            Some O(1) expressions
        }
    }
}

// while loop version
int i = 1;
while(i < n)
{
    int j = i + 1;
    while(j < n)
    {
        int k = i;
        while(k <= j)
        {
            Some O(1) expressions
            k = k + 1;
        }
        j = j + 1;
    }
    i = i + 1;
}

In the above three nested loops, the outer loop runs n - 1 time and two inner loops run n - i and j - i + 1 time. So what would be the total count of nested loop iterations? Let’s think.

       n - 1     n        j
T(n) =   ∑       ∑        ∑    O(1)
       i = 1  j = i + 1  k = i

Now we solve this tripple summation by expanding the summation one by one.

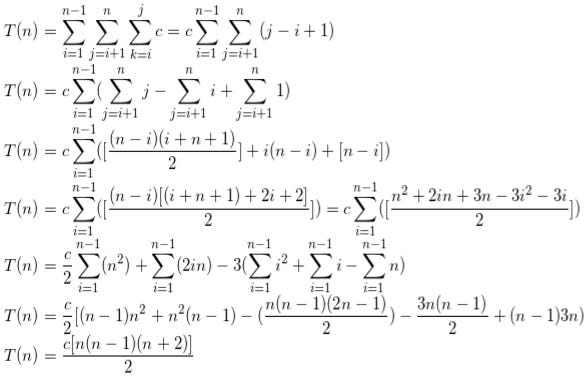
Higher-order term in T(n) is n^3, then T(n) = O(n^3). We are ignoring lower-order terms and coefficients.

Note: There is one error in the third line of the above image. Instead of + i(n - i), it would be - i (n - i).

We recommend to explore these coding problems to learn more about the time complexity analysis of loop

• Rotate a matrix by 90 degrees
• Print matrix in spiral order
• Detect loop in a linked List
• Sort a stack using another stack
• Implement queue using stacks
• Implement stack using queues
• Level order traversal of a binary tree 

If you have any queries or feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy coding, Enjoy algorithms!