Fenwick Tree (Binary Indexed Tree) Data Structure
Why Fenwick tree?
Suppose we are given an array of integer values and need to find the range sum between index i and j using one-based indexing. One way to solve this problem is to use a single loop. This approach has a time complexity of O(j - i), or O(n) in the worst case when j - i is equal to the length of the array, n. While this single-loop approach is easy to implement, it may not be the most efficient in terms of time complexity.
Now, suppose we need to find the range sum between any two indices in an array multiple times. One approach would be simply repeating the process described above for each query. However, in the worst case, this would result in a time complexity of m * O(n), or O(mn). This is a brute force approach, as it is inefficient and can take a long time if m and n are both large. Now the critical question is: Can we think of some other efficient strategy to improve the time complexity further?
If we have the prefix sum of the array up to indices 0 to i - 1 and 0 to j, we can easily calculate the range sum between indices i and j by subtracting the prefix sum of 0 to i-1 from the prefix sum of 0 to j i.e. Sum[i, j] = PrefixSum[0, j] - PrefixSum[0, i - 1]. This calculation will take O(1) time if we already have both values of the prefix sum.
However, if we have multiple range sum queries, we don't want to have to recalculate the prefix sum every time. One solution is to create a prefix sum array that stores the prefix sum of all indexes in the original array. This can be done using a single loop in O(n) time.
Once we have the prefix sum array, we can easily find the range sum between any two indices in O(1) time by using this formula: Sum between index [i, j] = PrefixSum[j] - PrefixSum[i - 1]. This allows us to efficiently answer multiple range sum queries without having to recalculate the prefix sum each time.
Python code for range sum query using prefix array
function construct_prefix_sum(array):
prefix_sum = [0]*(array.length + 1)
i = 1
while i <= array.length:
prefix_sum[i] = prefix_sum[i - 1] + array[i]
function range_query(i, j):
return prefix_sum[j] - prefix_sum [i - 1]
function update (i, val):
array[i] = val
construct_prefix_sum(array)However, there is another issue to consider when using a prefix sum array. Suppose we want to change the value of a single element in the original array. This can be done in O(1) time, but it would require us to reconstruct the prefix sum array in order to maintain its accuracy. This reconstruction process would take O(n) time.
Suppose, if there are m update queries and m range sum queries.
- The time complexity of update queries = m * time complexity of constructing prefix array = m * O(n) = O(mn).
- The time complexity of range sum queries = m * O(1) = O(m)
As we have seen, the prefix sum array solution has a faster time complexity for finding range sums (O(1)) but a slower time complexity for update queries (O(n)). On the other hand, the Fenwick tree solution has a slower time complexity for finding range sums (O(logn)) but a faster time complexity for update queries (O(logn)).
In situations where there are frequent update queries, the Fenwick tree solution may be more suitable as it has a faster time complexity for these queries. However, it is important to consider both the time complexity of update queries and finding range sums when deciding which solution is the most appropriate for a given situation.
Overall, the Fenwick tree solution offers a good trade-off between the time complexity of update queries and finding range sums, and may be a good choice in situations where there are frequent update queries.
What is Fenwick Tree?
The Fenwick tree, also known as a Binary Indexed Tree (BIT), is a data structure that was first described in a paper by Peter M. Fenwick in 1994. It is useful for efficiently calculating range sums and updating element values in an array.
Fenwick Tree Problem Description
Let arr[] be an array of integers of length n and f is a sum function for finding the range sum between any two indexes l and r. f(arr, l, r) = arr[l] + arr[l+1] + …… + arr[r].
The Fenwick tree has the following specifications:
- It can calculate the value of function f in the range [l, r] in O(logn) time.
- It can update the value of an element in arr in O(logn) time.
- It has a space complexity of O(n).
The following image represents the Fenwick tree.
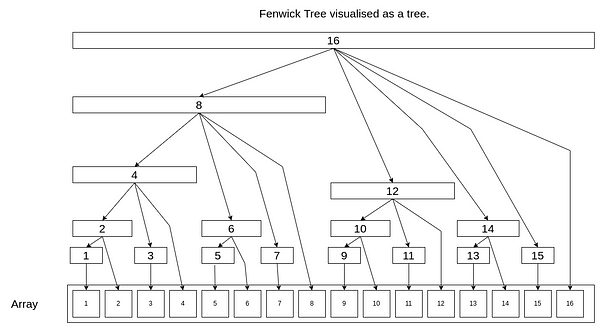
In a Fenwick tree, each cell is responsible for a range of other cells. The range of responsibility for a cell is determined by the position of the first non-zero bit from the right in the binary representation of the cell's index. This position is known as the rightmost set bit (RSB). The range of responsibility for a cell is equal to 2^(RSB - 1). Overall, the RSB of a cell in a Fenwick tree determines the range of responsibility of that cell and the cells below it. Note: It's important to note that the positions from the right are one-based in the Fenwick tree.
In the above Fenwick tree:
- The RSB for cell 1 is 1, so its range of responsibility is 2^(1 - 1) = 2^0 = 1. This means that cell 1 is responsible for itself.
- The RSB for cell 2 is 2 (binary representation of 2 is 10). So its range of responsibility is 2^(2 - 1) = 2^1 = 2. This means that cell 2 is responsible for itself and cell 1.
- The RSB for cell 4 is 3 (binary representation of 4 is 100). So its range of responsibility is 2^(3 - 1) = 2^2 = 4. This means that cell 4 is responsible for itself and cells 1, 2, and 3.
- The RSB for cell 12 is 3 (binary representation of 12 is 01100).So its range of responsibility is 2^(3 - 1) = 2^2 = 4. This means that cell 12 is responsible for itself and cells 9, 10, 11 and 12.
The following table represents the range of responsibility for numbers from 1 to 16.
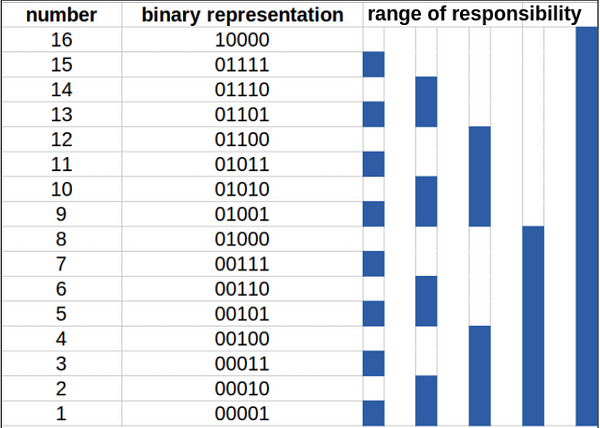
The Fenwick tree is a data structure that stores data in an array, even though it is called a tree. This is because each cell in the array is responsible for storing the sum of a range of elements in the original array. The cell at index i is responsible for storing the sum of elements from (g(i), i), where g(i) is the first index in the range of responsibility for cell i.
- fTree[i] = sum(array[j]), where j is from g(i) to i. This store the sum of elements in the range of responsibility for cell i.
- g(i) = 2^(RSB(i) - 1), where RSB(i) is the rightmost set bit in the binary representation of i.
Since the height of the Fenwick tree is log(n), the update and query operations take a maximum of log(n) time. This makes the Fenwick tree a useful data structure for efficiently performing range sum calculations and element updates in an array. Note: We will explain the construction of Fenwick tree later. For now, suppose we have our Fenwick tree ready.
Calculating range sum query using Fenwick Tree
To compute the prefix sum up to a specific index using a Fenwick tree, we can follow these steps:
- Initialize an answer variable with the value of fTree[i], where i is the index up to which we want to compute the prefix sum.
- Set a variable i equal to the index up to which we want to compute the prefix sum.
- Subtract the current range of responsibility for cell i from i. The current range of responsibility for a cell is determined by the rightmost set bit in the binary representation of the cell's index.
- Add the value of fTree[i] to the answer.
- Repeat steps 3 and 4 until the index i becomes 0.
For example, to find the prefix sum up to index 5, we would initialize the answer with fTree[5] and set i equal to 5. We would then subtract the current range of responsibility for cell 5 (which is 1) from i, resulting in i = 4. We would then add fTree[4] to the answer and subtract the current range of responsibility for cell 4 (which is 4) from i, resulting in i = 0. The final answer would be the sum of fTree[5] and fTree[4], which represents the prefix sum from index 1 to index 5 in the original array.
Similarly, do the same thing for finding prefix sum of [1, 15]. See the following table to understand how prefix sum up to 15 is calculated. The green regions are the ones that are used to find the answer.
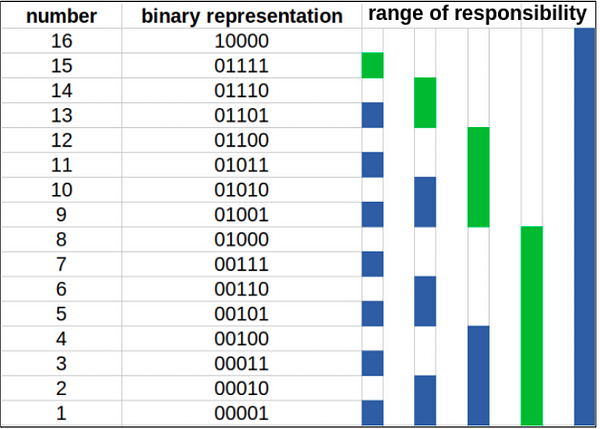
So to find the prefix sum up to index 15, the answer would be equal to the sum of fTree[15], fTree[14], fTree[12], and fTree[8]. This is because these cells are responsible for storing the sum of the elements in the range of responsibility for cell 15, which includes all elements from index 1 to index 15 in the original array.
The time complexity of computing the prefix sum using a Fenwick tree is O(log n), as we need a maximum of log(n) (the maximum number of set bits) operations to find the prefix sum. Once we have computed the prefix sum, we can use the formula rangeSum[i, j] = prefixSum[j] - prefixSum[i-1] to find the range sum for any range [i, j]. This formula takes O(1) time to compute.
Python code for fenwick tree range sum query
function prefix_sum(i):
sum = 0
while i > 0:
sum = sum + fTree[i]
i = i - g(i)
return sum
function range_query(i, j):
return prefix_sum(j) - prefix_sum(i - 1)Where g(i) returns the range of responsibility of i, where g(i) = 2^(RSB(i) - 1).
Point updates in Fenwick Tree
Point updates in a Fenwick tree involve adding a value to a single element in the original array and then propagating the change upwards through the tree to the cells responsible for the current cell. This is the opposite of performing a range query, which involves summing a range of values in the original array.
To perform a point update in a Fenwick tree, we can follow these steps:
- Identify the index of the element in the original array that you want to update.
- Add the value you want to update to the element at this index in the original array.
- Add range of responsibility the current index to the current index.
- Repeat step 3 until you reach the end of the tree.
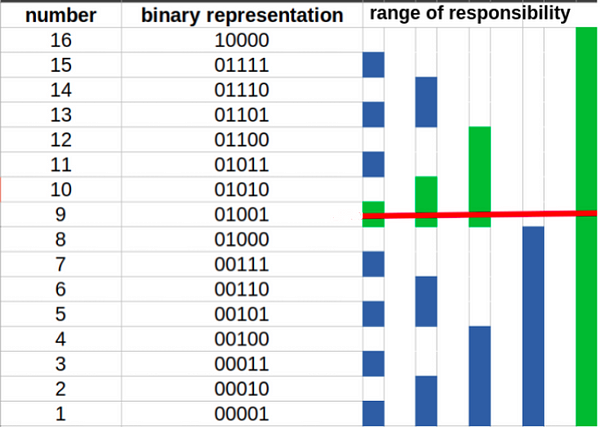
As you can see from the above image, if we want to update the value at index 9 by increasing the value in the original array at index 9 by x, we would have to propagate upwards from 9 to 10, 10 to 12, and 12 to 16. So the required updates are: fTree[9] += x, fTree[10] += x, fTree[12] += x, fTree[16] += x
For example, suppose we want to add 5 to the element at index 3 in the original array. We would first add 5 to the element at index 3 in the array, and then add range of responsibility of the index 3 (which is 2) to the current index (3) to obtain a new index 5. Now we add range of responsibility of index 5 (which is 3) to the current index (5) to obtain a new index 8. This process would continue until we reach the end of the tree.
By adding range of responsibility to the current index at each step, we are able to propagate the change upwards through the tree to the cells responsible for the current cell. This allows us to efficiently update the values in the tree and maintain the correct sum.
Python code for fenwick tree point update
function point_update(i, x):
array[i] = array[i] + x
while i < n:
fTree[i] = fTree[i] + x
i = i + g(i)The time complexity of the Fenwick tree point update is O(log n), similar to the prefix sum query. Think!
How to construct the Fenwick tree?
This is the first step that you have to do before answering any range sum or point update queries. You can create a tree with all values 0 initially and then do point updates for each index which will take O(nlogn) time, but we can do better and construct Fenwick tree in O(n) time.
The idea is to add the value in the current cell to the next immediate cell that is responsible for the current cell. It resembles the method for point updates but one cell at a time. This creates a cascading effect by propagating the value in each cell throughout the tree.
Let our current position be i. The immediate position responsible for i is i + g(i). We can consider cell i + g(i) as the parent of cell i. We must ignore this update if the parent cell is out of bounds.
To construct a Fenwick tree in linear time, we can follow these steps:
- Initialize the Fenwick tree with all values set to 0.
- Iterate through each element in the original array from left to right.
- For each element, add its value to the next immediate cell in the tree that is responsible for the current element. This cell is located at the index i + g(i), where i is the index of the current element and g(i) is the range of responsibility of i.
- If the parent cell (i + g(i)) is out of bounds, ignore this update.
Python code for construction of Fenwick tree
function build(array):
n = len(array)
fTree = array.copy()
for i = 1 to n:
j = i + g(i)
if j < n:
fTree[j] = fTree[j] + fTree[i]
return fTreeHow does RSB work?
The RSB of a number is the rightmost set bit in the binary representation of that number. We can find the RSB by using the bitwise AND operator with the negative of the number. This works because the negative of a number is produced by inverting the bits of the number and then adding 1 (using two's complement representation). When we add 1, every bit starting at the bottom will overflow into the next higher bit until we reach a bit that is already set to 1. These overflowed bits will all be 0, and the bits above the last one affected will be the inverse of each other. The only bit left that is set to 1 is the one that stopped the cascade, which is the RSB of the original number.
// returns the range of responsibility of index i
private static int g(int i)
{
return i & -i;
}The above explanation was for range queries and point updates. We can also use the Fenwick tree for range updates and point queries and range updates and range queries. We will briefly explain the modifications we need to do for each of these cases.
Range updates and point queries
The Fenwick tree is initialized with zeros. Suppose we want to increment the interval [l, r] by x. We need to make two point update operations on the Fenwick tree: point_update(l, x) and point_update(r + 1, -x). After these operations, the values from 0 to i < l have no effect. The values from l <= i <= r are incremented by x. And if i > r, then the second update operation will cancel the effect of the first one.
Thus, to get the value of arr[i], we take the prefix sum using the range sum method.
Range updates and range queries
To handle both range updates and range queries, we require 2 Fenwick Trees, fTree1 and fTree2, initialized with zeros. If we want to do a range update query, we can do it as follows:
function range_update(l, r, x):
point_update(fTree1, l , x)
point_update(fTree1, r + 1, -x)
point_update(fTree2, l , x * (l - 1))
point_update(fTree1, r + 1, -x * r)After a range update query range_update(l, r, x), the value of prefixSum(i) for a given i is determined by the following conditions:
- If i < l, then prefixSum(i) = 0.
- If l <= i <= r, then prefixSum(i) = x * (i - (l - 1)).
- If i > r, then prefixSum(i) = x * (r - (l + 1)).
This can also be expressed more concisely as follows:
- If i < l, then prefixSum(i) = 0 * i - 0.
- If l <= i <= r, then prefixSum(i) = x * i - x * (l - 1).
- If i > r, then prefixSum(i) = 0 * i - (x * (l - 1) - x * r).
Finally, we can express prefixSum(i) as a function of fTree1 and fTree2 as follows: prefixSum(i) = (prefixSum(fTree1, i) * i) - prefixSum(fTree2, i).
Fenwick Tree Java Implementation
class Fenwick
{
private final int n;
private int[] tree;
private int[] array;
//initialise tree
public Fenwick(int n)
{
this.n = n + 1;
this.tree = new int[this.n];
this.array = new int[this.n];
}
public Fenwick(int[] values)
{
this.n = values.length + 1;
this.array = new int[n];
for(int i = 1; i < this.n; i = i + 1)
array[i] = values[i - 1];
tree = array.clone();
for (int child = 1; child < n; child = child + 1)
{
int parent = child + g(child);
if (parent < n)
tree[parent] = tree[parent] + tree[child];
}
}
//update values of array[index] to val
//delta = newVal - previousVal
// zero based indexing in argument
public void update(int index, int val)
{
index = index + 1;
int delta = val - array[index];
array[index] = val;
int pos = index;
while(pos < n)
{
tree[pos] = tree[pos] + delta;
pos = pos + g(pos);
}
}
// increment value of array[index] by delta
// zero based indexing in argument
public void increment(int index, int delta)
{
index = index + 1;
array[index] = array[index] + delta;
int pos = index;
while(pos < n)
{
tree[pos] = tree[pos] + delta;
pos = pos + g(pos);
}
}
// find prefixSum till index
// one based indexing in argument
public int prefixSum(int index)
{
int ans = 0;
while (index != 0)
{
ans = ans + tree[index];
index = index - g(index);
}
return ans;
}
// returns the range of responsibility of index i
private static int g(int i)
{
return i & -i;
}
}
class FenwickRangeQueryPointUpdate extends Fenwick
{
FenwickRangeQueryPointUpdate(int n)
{
super(n);
}
FenwickRangeQueryPointUpdate(int [] values)
{
super(values);
}
// range query from index l to r
// zero based indexing in argument
public int query(int left, int right)
{
return prefixSum(right + 1) - prefixSum(left);
}
}
class FenwickPointQueryRangeUpdate
{
private Fenwick fTree;
private int length_arr;
//initialise tree
FenwickPointQueryRangeUpdate(int n, int [] array)
{
this.fTree = new Fenwick(n);
this.length_arr = n;
for(int i = 0; i < n; i = i + 1)
{
int delta = array[i];
fTree.increment(i, delta);
if(i + 1 < length_arr)
fTree.increment(i + 1, -delta);
}
}
// increment the values from index l to r by delta
// zero based indexing in argument
public void range_update(int left, int right, int delta)
{
fTree.increment(left, delta);
if(right + 1 < length_arr)
fTree.increment(right + 1, -delta);
}
// return value of index
// zero based indexing in argument
public int point_query(int index)
{
return fTree.prefixSum(index + 1);
}
}
class FenwickRangeQueryRangeUpdate
{
private Fenwick fTree1, fTree2;
private int length_arr;
//intialise 2 Fenwick Trees
public FenwickRangeQueryRangeUpdate(int n, int [] array)
{
this.fTree1 = new Fenwick(n);
this.fTree2 = new Fenwick(n);
this.length_arr = n;
for(int i = 0; i < n; i = i + 1)
{
int delta = array[i];
fTree1.increment(i, delta);
if(i + 1 < length_arr)
fTree1.increment(i + 1, -delta);
fTree2.increment(i, delta*(i - 1));
if(i + 1 < length_arr)
fTree2.increment(i + 1, -delta*i);
}
}
// increment the values from index l to r by delta
// zero based indexing in argument
public void increment(int left, int right, int delta)
{
fTree1.increment(left, delta);
if(right + 1 < length_arr)
fTree1.increment(right + 1, -delta);
fTree2.increment(left, delta*(left - 1));
if(right + 1 < length_arr)
fTree2.increment(right + 1, -delta*right);
}
// range query from index l to r
// zero based indexing in argument
public int query(int left, int right)
{
return prefixSum(right + 1) - prefixSum(left);
}
// find prefixSum till index
// one based indexing in argument
public int prefixSum(int index)
{
return fTree1.prefixSum(index) * (index - 1) - fTree2.prefixSum(index);
}
} Fenwick Tree Python Implementation
class Fenwick:
def __init__(self, length, array = []):
# initialise tree
self.length = length + 1
self.tree = [0 for pos in range(self.length)]
if array != []:
self.array = [0] + array
# one based indexing
for i in range(1, self.length):
self.tree[i] = self.array[i]
for child in range(1, self.length):
parent = child + self.g(child)
if parent < self.length:
self.tree[parent] += self.tree[child]
else:
self.array = [0 for i in range(self.length)]
def update(self, index, val):
# update values of arr[index] to val
# delta = newVal - previousVal
# zero based indexing in argument
index += 1
delta = val - self.array[index]
self.array[index] = val
pos = index
while pos < self.length:
self.tree[pos] += delta
pos += self.g(pos)
def increment(self, index, delta):
# increment value of arr[index] by delta
# zero based indexing in argument
index += 1
self.array[index] += delta
pos = index
while pos < self.length:
self.tree[pos] += delta
pos += self.g(pos)
def prefixSum(self, index):
# find prefixSum till index
# one based indexing in argument
ans = 0
while index != 0:
ans += self.tree[index]
index -= self.g(index)
return ans
def g(self, i):
# returns the rightmost set bit
return i & -i
class FenwickRangeQueryPointUpdate(Fenwick):
def query(self, right, left = 0):
# range query from index l to r
# zero based indexing in argument
return self.prefixSum(right + 1) - self.prefixSum(left)
class FenwickPointQueryRangeUpdate:
def __init__(self, length, array = []):
# initialise tree
self.fTree = Fenwick(length, [])
self.length_arr = length
for i in range(self.length_arr):
delta = array[i]
self.fTree.increment(i, delta)
if i + 1 < self.length_arr:
self.fTree.increment(i + 1, -delta)
def range_update(self, left, right, delta):
# increment the values from index l to r by delta
self.fTree.increment(left, delta)
if right + 1 < self.length_arr:
self.fTree.increment(right + 1, -delta)
def point_query(self, index):
# return value of index
return self.fTree.prefixSum(index + 1)
class FenwickRangeQueryRangeUpdate:
def __init__(self, length, array = []):
# intialise 2 Fenwick Trees
self.fTree1 = Fenwick(length, [])
self.fTree2 = Fenwick(length, [])
self.length_arr = length
for i in range(self.length_arr):
delta = array[i]
self.fTree1.increment(i, delta)
if i + 1 < self.length_arr:
self.fTree1.increment(i + 1, -delta)
self.fTree2.increment(i, delta*(i - 1))
if i + 1 < self.length_arr:
self.fTree2.increment(i + 1, -delta*i)
def increment(self, left, right, delta):
# increment the values from index l to r by delta
self.fTree1.increment(left, delta)
if i + 1 < self.length_arr:
self.fTree1.increment(right + 1, -delta)
self.fTree2.increment(left, delta*(left - 1))
if i + 1 < self.length_arr:
self.fTree2.increment(right + 1, -delta*right)
def query(self, right, left):
# range query from index l to r
return self.prefixSum(right + 1) - self.prefixSum(left)
def prefixSum(self, index):
# find prefixSum till index
return self.fTree1.prefixSum(index) * (index-1) - self.fTree2.prefixSum(index)Please write in the message below if you find anything incorrect, or you want to share more insight. Enjoy learning, Enjoy algorithms.
Share Your Insights
More from EnjoyAlgorithms
Self-paced Courses and Blogs
Coding Interview
OOP Concepts
Our Newsletter
Subscribe to get well designed content on data structure and algorithms, machine learning, system design, object orientd programming and math.
©2023 Code Algorithms Pvt. Ltd.
All rights reserved.
