Check whether an array is a subset of another array

Difficulty: Medium, Asked-in: Amazon, Qualcomm

Key takeaway: An excellent problem to learn problem-solving and time complexity optimization using various approaches.

Let’s understand the problem

Given two unsorted arrays X[] and Y[] of size m and n respectively, write a program to check whether array Y[] is a subset of array X[] or not. Y[] will be a subset of X[] if each element of Y[] is present in X[]. Assume that there are no repeated elements in both arrays and n <= m.

Example 1

Input: X[] = [2, 8, 12, 6, 10, 11], Y[] = [8, 2, 6, 11], Output: true

Explanation: All elements of Y[] are present in X[]. So Y[] is a subset of X[].

Example 2

Input: X[] = [6, 4, 8, 3, 2], Y[] = [4, 7, 3, 9], Output: false

Explanation: 7 and 9 of Y[] are not present in X[]. So Y[] is not a subset of X[].

Discussed solution approaches

• Brute force approach using linear search
• Using sorting and binary search
• Using sorting and two pointers approach
• Efficient approach using a hash table

Brute force approach  using linear search

Solution idea

A basic idea would be to search each Y[] element in X[] using linear search. When we find the first element Y[i] not present in X[], then Y[] is not a subset of X[], and we return false. Otherwise, If all Y[] elements are present in X[], then Y[] is a subset of X[], and we return true.

Solution code C++

int linearSearch(int X[], int l, int r, int key)
{
    for (int i = l; i <= r; i = i + 1)
    {
        if (X[i] == key)
            return i;
    }
    return -1;
}

bool checkSubsetArray(int X[], int m, int Y[], int n)
{
    int i = 0;
    while (i < n)
    {
        int k = linearSearch(X, 0, m - 1, Y[i]);
        if (k == -1)
            return false;
        else 
            i = i + 1;    
    }
    return true;
}

Solution code Python

def linearSearch(X, l, r, key):
    for i in range(l, r + 1):
        if X[i] == key:
            return i
    return -1

def checkSubsetArray(X, m, Y, n):
    i = 0
    while i < n:
        k = linearSearch(X, 0, m - 1, Y[i])
        if k == -1:
            return False
        else:
            i = i + 1
    return True

Solution analysis

In worst case, we are searching n elements of Y[] linearly in array X[] of size m. So time complexity in worst-case = O(n) * O(m) = O(mn).

If we observe closely, time complexity depends on the order of elements in both arrays. So what would be the best and worst scenarios? Think! We are using constant extra space, so space complexity = O(1).

Using sorting and binary search

Searching is one of the critical operations for solving this problem. The critical question is: Can we improve efficiency of searching operation to improve overall time complexity?

Solution idea

We can think to apply binary search, which works in O(logn) time on the sorted array of size n. So if we sort larger array X[], we can apply binary search to search each element of Y[] efficiently.

Suppose for the implementation, we use one of the fastest O(nlogn) sorting algorithms heap sort or quick sort, and iterative binary search.

Solution steps

• Sort X[] in increasing order.
• Now run a loop from i = 0 to n - 1 and search each Y[i] in X[] using binary search. If Y[i] is not present in X[], we return false. Otherwise, we move to the next element in Y[] and repeat the same process.
• If the above loop reaches its end, then all Y[] elements will be present in X[], and we return true.

Solution code C++

int binarySearch(int X[], int l, int r, int key)
{ 
    while (l <= r) 
    { 
        int mid = l + (r - l) / 2;
        if (X[mid] == key) 
            return mid;
        if (X[mid] < key) 
            l = mid + 1;
        else
            r = mid - 1;
    }
    return -1;
}

bool checkSubsetArray(int X[], int m, int Y[], int n)
{
    sort(X, X + m);
    for (int i = 0; i < n; i = i + 1)
    {
        int k = binarySearch (X, 0, m - 1, Y[i]);
        if (k == -1)
            return false;
    }
    return true;
}

Solution code Python

def binarySearch(X, l, r, key): 
    while l <= r: 
        mid = l + (r - l) // 2
        if X[mid] == key: 
            return mid
        if X[mid] < key: 
            l = mid + 1
        else:
            r = mid - 1
    return -1

def checkSubsetArray(X, m, Y, n):
    X.sort()
    for i in range(n):
        k = binarySearch(X, 0, m - 1, Y[i])
        if k == -1:
            return False
    return True

Solution analysis

Time complexity = Time complexity of sorting + n * Time complexity of binary search = O(mlogm) + n. O(logm) = O(mlogm + nlogm). Here m > n, then mlogm > nlogm. So O(mlogm + nlogm) = O(mlogm).

Space complexity = Space complexity of sorting + Space complexity of binary search.

If we use heap sort and iterative binary search, space complexity = O(1) + O(1) = O(1).

If we use merge sort and iterative binary search, space complexity = O(m) + O(1) = O(m).

Using sorting and two pointers approach

Solution idea and steps

Sometimes two pointers approach works perfectly on sorted arrays. How do we apply this approach? Here is an idea: Sort both arrays and think to apply two-pointers approach. How? Let's think!

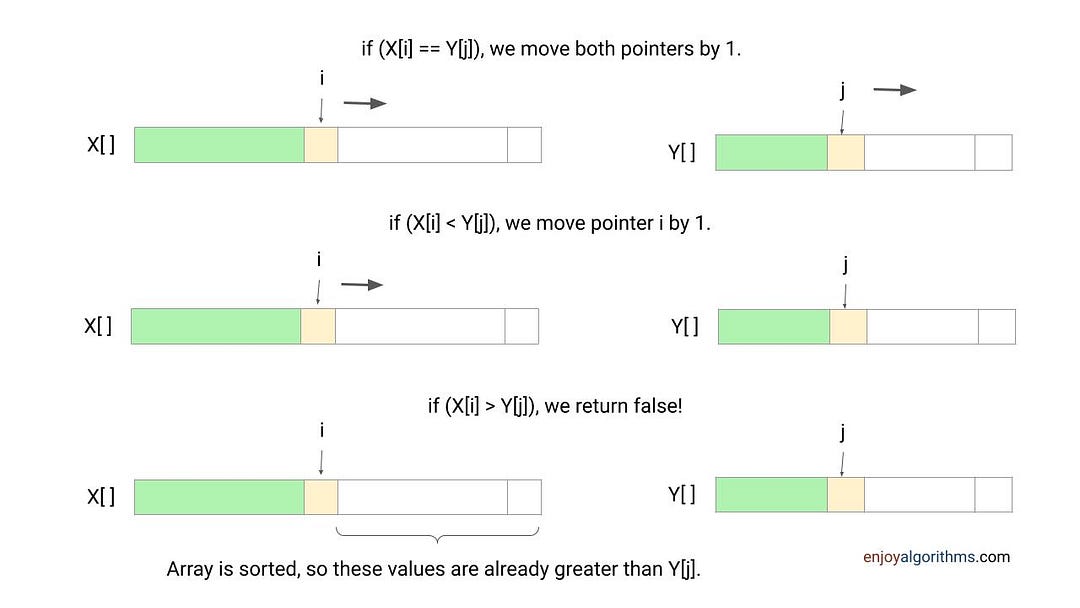
Suppose we sort X[] and Y[] and initialize two pointers i and j i.e. i = 0 and j = 0. Now we move both pointers and track common elements by comparing elements in both arrays. During this process, we increment pointers based on the following three conditions. Note: This loop will run till any one of the pointers reaches the end i.e. i < m && j < n.

if (X[i] == Y[j]): We found an element present in both arrays. So we move pointers i and j by 1.

if(X[i] < Y[j]): We have not yet found element Y[j] in X and it may be present in the remaining part of X[]. So we move pointer i by 1.

if(X[i] > Y[j]): We can say that Y[j] is not present in X at all and we return false. The idea is simple: Both arrays are sorted, so the remaining elements of X[] will be definitely greater than Y[j].

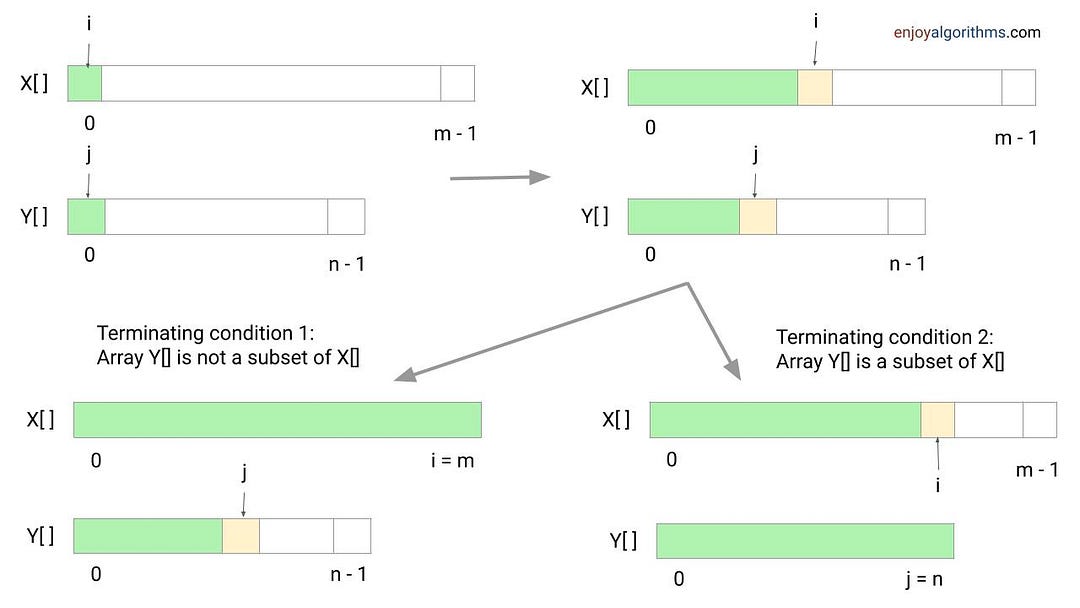
Boundary condition: If we exit the above loop due to condition i == n, it means pointer j has not reached the end. In this situation, remaining values in Y (from pointer j to n - 1) will not be present in X[]. So both arrays are not subset of each other, and we return false. Otherwise, if we exit the loop due to condition j == n, then each value of Y[] is present in X[], and we return true. Think!

Solution code C++

bool checkSubsetArray(int X[], int m, int Y[], int n)
{
    sort(X, X + m);
    sort(Y, Y + n);
    int i = 0, j = 0;
    while (i < m && j < n)
    {
        if (X[i] < Y[j])
            i = i + 1;
        else if(X[i] == Y[j])
        {
            j = j + 1;
            i = i + 1;
        }
        else if(X[i] > Y[j])
           return false;
    }
    if (j < n)
        return false;
    else
        return true;
}

Solution code Python

def check_subset_array(X, m, Y, n):
    X.sort()
    Y.sort()
    i = 0
    j = 0
    while i < m and j < n:
        if X[i] < Y[j]:
            i = i + 1
        elif X[i] == Y[j]:
            i = i + 1
            j = j + 1
        else:
            return False
    if j < len(Y):
        return False
    else:
        return True

Solution analysis

At each iteration, we compare one element from X and Y. In other words, we increment pointer i or j or both by 1, depending on comparison. So total number of comparisons in worst case = m + n, and time complexity of two pointers while loop = O(m + n).

If we observe closely, comparison count depends on the order of elements in both arrays. So what would be the best and worst scenarios? Think!

Suppose we use an efficient O(nlogn) sorting algorithm like heap sort or merge sort for the implementation. So overall time complexity = Time complexity to sort X[] + Time complexity to sort Y[] + Time complexity of two pointers loop = O(mlogm) + O(nlogn) + O(m + n) = O(mlogm + nlogn).

Here m > n, O(mlogm + nlogn) = O(mlogm).

Space complexity = Space complexity to sort X[] + Space complexity to sort Y[] + Space complexity of two pointers loop.

If we use heap sort, space complexity = O(1) + O(1) + O(1) = O(1). If we use merge sort, space complexity = O(m) + O(n) + O(1) = O(m + n).

Efficient approach  using a hash table

Now critical questions are: Can we improve the time complexity to O(n)? Can we solve the problem without using sorting? Think!

Solution idea

Searching is essential in the problem because we need to search each Y[] value in X[]. So, we can think of improving time complexity by using an efficient data structure for searching i.e. hash table. Hash table performs searching and insertion efficiently in O(1) time average.

Solution steps

• Take a hash table of size O(m).
• Insert all elements of X[] into the hash table.
• Now traverse Y[] and search each element Y[i] in the hash table. Return false if any element Y[i] is not present in the hash table.
• If we find all Y[] elements in the hash table, return true.

Solution pseudocode

int checkSubset(int X[], int Y[], int m, int n)
{
    HashTable H
    for (int i = 0; i < m; i = i + 1)
        H.insert(X[i])
    for (int i = 0; i < n; i = i + 1)
    {
        if (H.search(Y[i]) == false)
            return false
    }
    return true
}

Solution code C++

bool checkSubset(int X[], int m, int Y[], int n) 
{
    unordered_map<int, bool> H;
    for (int i = 0; i < m; i = i + 1)
        H.insert({X[i], true});

    for (int i = 0; i < n; i = i + 1) 
    {
        if (H.find(Y[i]) == H.end())
            return false;
    }
    
    return true;
}

Solution code Python

def check_subset(X, m, Y, n):
    H = defaultdict(bool)
    for i in range(m):
        H[X[i]] = True
    for i in range(n):
        if Y[i] not in H:
            return False
    return True

Solution code Java

class Solution 
{
    public boolean checkSubset(int[] X, int m, int[] Y, int n) 
    {
        HashMap<Integer, Boolean> H = new HashMap<>();
        for (int i = 0; i < m; i = i + 1)
            H.put(X[i], true);

        for (int i = 0; i < n; i = i + 1) 
        {
            if (H.containsKey(Y[i]) == false)
                return false;
        }
        
        return true;
    }
}

Solution analysis

Time complexity = Time complexity of inserting m elements of X[] in hash table + Time complexity of searching n elements of Y[] in hash table = m. O(1) + n . O(1) = O(m) + O(n) = O(m + n)

Space complexity = Extra space for the hash table = O(m)

Critical ideas to think!

• In comparison to 2nd and 3rd approaches, which one is more efficient in terms of time complexity?
• Can above algorithm works fine if elements are repeated?
• Can we solve this problem using some other approach?
• In 2nd approach, can we solve the problem by sorting smaller array Y[]?
• In last approach, what will be time and space complexity if we use self-balancing BST in place of hash table?
• What would be the worst and best case input in brute force approach? Try to count exact number of comparison operations in worst-case scenario.
• What would be worst-case input in the two-pointers approach? Try to count the exact number of comparison operations in the worst-case scenario.
• What would be time and space complexity if we use quick-sort in 2nd and 3rd approaches?
• Why the idea of the two-pointer approach works perfectly for a sorted array? Verify correctness of the 3rd approach.

Comparisons of time and space complexities

• Nested loops: Time = O(nm), Space = O(1)
• Sorting and binary search: Time = O(mlogm + nlogm), Space = O(1)
• Sorting and two pointers: Time = O(mlogm + nlogn), Space = O(1)
• Hash Table approach: Time = O(m + n), Space = O(m)

Suggested coding problems to practice

• Move zeroes to an end
• Check pair in an array with given sum
• The intersection of unsorted arrays
• Remove duplicates from sorted array
• Container With Most Water
• Trapping Rain Water

Enjoy learning, Enjoy algorithms!