Climbing Stairs Problem
Difficulty: Medium, Asked-in: Google, Amazon, Intel, Morgan Stanley, LinkedIn
Key takeaway: An excellent problem to learn problem-solving using dynamic programming and application of the Fibonacci series. One can find a lot of similar DP problems asked during the coding interview.
Let’s understand the problem
There is a staircase of n steps and you can climb either 1 or 2 steps at a time. We need to count and return total number of unique ways to reach the n'th stair. The order of steps matters.
Example 1
Input: n = 3, Output: 3
Explanation: There are 3 unique ways of climbing the staircase: [1,1,1], [2,1] and [1,2]
Example 2
Input: n = 5, Output: 8
Explanation: There are 8 unique ways of climbing the staircase: [1,1,1,1,1], [1,1,1,2], [1,1,2,1], [1,2,1,1], [2,1,1,1], [1,2,2], [2,1,2], [2,2,1]
Discussed solution approaches
- Brute force approach using recursion
- Using bottom-up approach of dynamic programming
- Using the idea of Fibonacci sequence
- Using Binet’s method of matrix exponentiation
Brute force approach using recursion
Solution idea
This is a counting problem where we need to count all unique ways to reach the nth stair. The critical question is: how do we count all possibilities?
We have two different choices at the start: we can either climb the 1st stair or the 2nd stair because we can only jump 1 or 2 steps at a time.
- If we take one step from the ground, the smaller sub-problem is climbing the nth stair from the 1st stair.
- If we take two steps from the ground, the smaller sub-problem is climbing the nth stair from the 2nd stair.
- Therefore, we can solve the given counting problem recursively by adding the solutions of the sub-problems: climbingStairs(0, n) = climbingStairs(1, n) + climbingStairs(2, n).
We can also think of it with another analogy: we can reach the nth stair from the (n - 1)th stair and the (n - 2)th stair by taking 1 and 2 steps, respectively. So the total number of ways to reach the nth stair is equal to the total number of ways to reach the (n - 1)th stair plus the total number of ways to reach the (n - 2)th stair => climbingStairs(n) = climbingStairs(n-1) + climbingStairs(n-2).
Solution code C++
int climbingStairs(int i, int n)
{
if (i > n)
return 0;
if (i == n)
return 1;
return climbingStairs(i + 1, n) + climbingStairs(i + 2, n);
}
int countClimbStairs(int n)
{
return climbingStairs(0, n);
}Solution code Python
def climbingStairs(i, n):
if i > n:
return 0
if i == n:
return 1
return climbingStairs(i + 1, n) + climbingStairs(i + 2, n)
def countClimbStairs(n):
return climbingStairs(0, n)Time and space complexity analysis
Input size of the original problem = n. Input size of the 1st subproblem = n - 1. Input size of the 2nd subproblem = n - 2. So, we write the recurrence relation of the time complexity in terms of the input size, i.e., T(n) = T(n - 1) + T(n - 2), where T(1) = 1 and T(2) = 2.
The above recurrence relation is similar to the recurrence relation of the Fibonacci sequence. So time complexity is O(2^n). Think! There is another rough analogy: we have two choices with each stair (excluding the 0th and nth), i.e., either we include it in the solution or exclude it. The total number of possibilities is approximately 2^n, so the time complexity is O(2^n).
But why is the time complexity in exponential order? We can visualize it better using a recursion tree diagram, where we are solving the same subproblem again and again during recursion. Here is a basic example for n = 4.
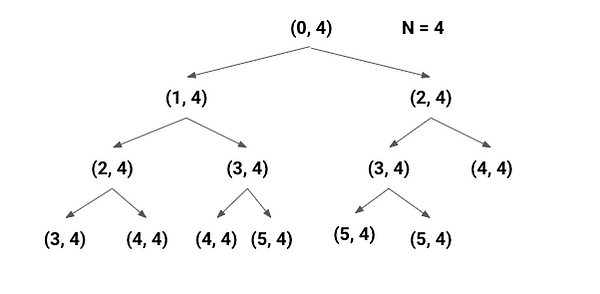
Space complexity = O(n), The depth of recursion tree can go up to n and recursion will allocate call stack of size O(n). Think!
Using bottom-up approach of dynamic programming
Solution idea and steps
Since overlapping subproblems are present in this scenario, we can optimize the solution using dynamic programming. Here we solve each subproblem once, store the results in extra memory, and retrieve their results in O(1) instead of calculating them again. We need to take care of the following steps to solve the problem using a bottom-up approach:
- Table size and structure: There are (n+1) different subproblems with input sizes from 0 to n. So we need to take a stair[] table of size n + 1 to store the solution to these subproblems.
- Table Initialization: Before building the solution in a bottom-up manner, we initialize the table by using the basic version of the solution. We can get this idea from the base case of the recursive solution. stair[1] = 1, stair[2] = 2.
-
Iterative structure to fill the table: Now we define an iterative structure to fill the table or build the solution in a bottom-up manner. We can get this idea from the recursive structure of the recursive solution. Here is an insight: Recursion is coming top-down and solving the larger problem via the solution of smaller subproblems. In a similar but reverse fashion, we need to go bottom-up and combine smaller problems to build the solution for the larger problem.
The total number of ways to reach the ith stair = The total number of ways to reach the (i - 1)th stair + The total number of ways to reach the (i - 2)th stair => stair[i] = stair[i-1] + stair[i-2]
- Returning the final solution: After storing the results in the table, our final solution gets stored at the last index of the array, i.e., return stair[n].
Solution code C++
int climbingStairs(int n)
{
if (n == 0)
return 0;
int stair[n + 1];
stair[1] = 1;
stair[2] = 2;
for (int i = 3; i <= n; i = i + 1)
stair[i] = stair[i - 1] + stair[i - 2];
return stair[n];
}Solution code Python
def climbingStairs(n):
if n == 0:
return 0
stair = [0] * (n + 1)
stair[1] = 1
stair[2] = 2
for i in range(3, n + 1):
stair[i] = stair[i - 1] + stair[i - 2]
return stair[n]Time and space complexity analysis
We are running a single loop and doing constant operations at each step of the iteration, so the time complexity is O(n). The space complexity is also O(n) because we are using extra space of size n+1.
Using Fibonacci sequence
Solution idea
If we observe the above approaches, the recursive and iterative structures are similar to the expression of the Fibonacci series. So rather than using recursion or using extra memory to store the solution of subproblems, we can think to apply the in-place solution to find the nth number of the Fibonacci series, where 1 and 2 are the first and second terms respectively.
fib(n) = fib(n-1) + fib(n-2), where fib(1) = 1 and fib(2) = 2.
Solution code C++
int climbingStairs(int n)
{
if (n == 0 || n == 1)
return n;
int firstFib = 1;
int secondFib = 2;
for (int i = 3; i <= n; i = i + 1)
{
int nextFib = firstFib + secondFib;
firstFib = secondFib;
secondFib = nextFib;
}
return secondFib;
}Solution code Python
def climbingStairs(n):
if n == 0 or n == 1:
return n
firstFib = 1
secondFib = 2
for i in range(3, n + 1):
nextFib = firstFib + secondFib
firstFib = secondFib
secondFib = nextFib
return secondFibTime and space complexity analysis
We are just running a single loop and doing constant operations at each step of the iteration, so the time complexity is O(n). The space complexity is O(1) because we are only using a constant number of variables.
Using Binet’s method of matrix exponentiation
Solution idea
This is an efficient method to find the nth Fibonacci number, which uses this idea: if we multiply the matrix M = [[1,1],[1,0]] n times or calculate power(M, n), then we get the (n+1)th Fibonacci number as the element at the 0th row and 0th column, i.e., at the position (0, 0) in the final matrix.
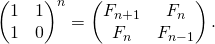
We can apply the above method because the recurrence relation of this problem is similar to the Fibonacci sequence. The only change we need to do is to modify the base case to 1 and 2 instead of 0 and 1 in the Fibonacci series.
So, we can use the same initial matrix M and return the element at index (0,0) of the matrix M^n i.e. the (n+1)th Fibonacci number. We can do this because the nth term of the recurrence relation is equal to the (n+1) th Fibonacci number (Base cases are the 2nd and 3rd terms of the normal Fibonacci series).
Solution pseudocode
int countWaysToClimbStairs(int n)
{
int M[][] = [[1, 1], [1, 0]]
int finalMatrix[][] = power(M, n)
return finalMatrix[0][0]
}
int[][] power(int X[][], int n)
{
int res[][] = [[1, 0], [0, 1]]
while (n > 0)
{
if (n % 2 == 1)
res = multiply(res, X)
X = multiply(X, X)
n = n/2
}
return res
}
int[][] multiply(int A[][], int B[][])
{
int C[][] = new int[2][2]
for (int i = 0; i < 2; i = i + 1)
{
for (int j = 0; j < 2; j = j + 1)
C[i][j] = A[i][0] * B[0][j] + A[i][1] * B[1][j]
}
return C
}Solution code C++
vector<vector<int>> multiply(vector<vector<int>> A, vector<vector<int>> B)
{
vector<vector<int>> C(2, vector<int>(2));
for (int i = 0; i < 2; i = i + 1)
{
for (int j = 0; j < 2; j = j + 1)
C[i][j] = A[i][0] * B[0][j] + A[i][1] * B[1][j];
}
return C;
}
vector<vector<int>> power(vector<vector<int>> X, int n)
{
vector<vector<int>> res = {{1, 0}, {0, 1}};
while (n > 0)
{
if (n % 2 == 1)
res = multiply(res, X);
X = multiply(X, X);
n = n / 2;
}
return res;
}
int countWaysToClimbStairs(int n)
{
vector<vector<int>> M = {{1, 1}, {1, 0}};
vector<vector<int>> finalMatrix = power(M, n);
return finalMatrix[0][0];
}Solution code Python
def multiply(A, B):
C = [[0, 0] for i in range(2)]
for i in range(2):
for j in range(2):
C[i][j] = A[i][0] * B[0][j] + A[i][1] * B[1][j]
return C
def power(X, n):
res = [[1, 0], [0, 1]]
while n > 0:
if n % 2 == 1:
res = multiply(res, X)
X = multiply(X, X)
n = n // 2
return res
def count_ways_to_climb_stairs(n):
M = [[1, 1], [1, 0]]
final_matrix = power(M, n)
return final_matrix[0][0]Time and space complexity analysis
- The time complexity of 2x2 matrix multiplication is O(1) (Think!)
- Inside the power() function, the while loop will run logn times, so the multiply() function is called logn number of times. Therefore, time complexity = O(logn) * O(1) = O(logn)
- We are only using a constant-size extra matrix res[2][2] for the calculation of the nth power of the matrix. Therefore, space complexity = O(1)
Critical ideas to think!
- Can we solve this problem using any other approach?
- How do we modify the above algorithms if we can climb up to k steps at a time? What would be the recurrence relation for this?
- How will the solution change if the order of steps you take didn’t matter? In this case, {1,1,2}, {1,2,1}, and {2,1,1} will be counted as one solution.
- Explore the correctness proof of the matrix exponentiation approach.
Comparison of time and space complexities
- Brute force recursive approach: Time = O(2^n), Space = O(n)
- Using the bottom-up approach of DP: Time = O(n), Space = O(n)
- Using the Fibonacci sequence: Time = O(n), Space = O(1)
- Binet’s method of matrix exponentiation: Time = O(logn), Space = O(1)
Similar coding problems to practice
- Find the number of ways to climb N stairs by taking at most k steps.
- Find the nth Fibonacci Number.
- Count the number of ways to reach the nth stair using steps 1, 2, or 3.
- Consider a game where a player can score 3, 5, or 10 points in a move. Given a total score of n, find the number of ways to reach the given score.
- Given n, count the number of ways to express n as a sum of 1, 3, and 4.
- Count the number of paths from the top left corner to the bottom right corner of an MxN grid, where you can only move down or right.
- Given a set of distinct integers, find all possible subsets that add up to a target sum.
If you have any queries/doubts/feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!