Representation of Graph in Data Structures

Why is understanding the representation of graphs important? One of the key reasons is that it helps us efficiently model real-life graph problems based on various properties and constraints. In other words, several fundamental properties of graphs impact the choice of data structures used to represent them. So, let’s move forward to understand this idea!

Just like other data structures, we can represent graphs using sequential and list representations: Adjacency list and adjacency matrix. We can apply both representations to model directed and undirected graphs.

Adjacency List Representation of Graph

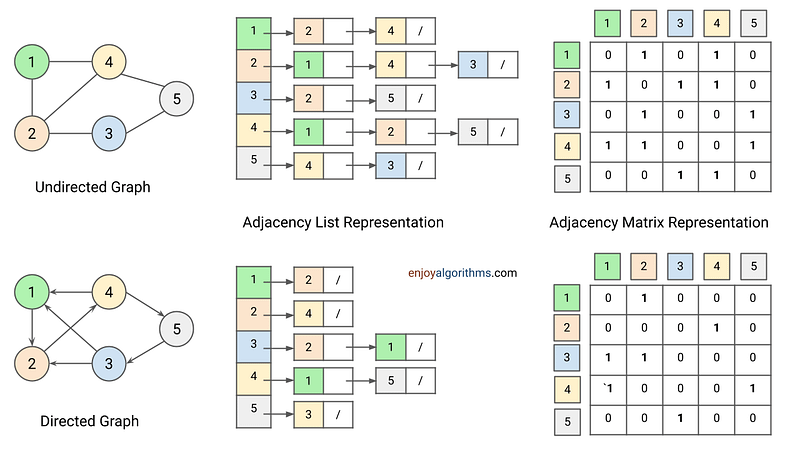
In the adjacency-list representation, we create an array Adj[V] of size V, where each array element represents a graph vertex, and the array index corresponds to the vertex itself. On the other side, for each vertex u, Adj[u] is a list (array or linked list) that contains all the vertices adjacent to vertex u. So, the elements within the list at Adj[u] represent vertices that share an edge with vertex u. In other words, for each vertex v in Adj[u], there is an edge (u, v) in the graph.

Now, let’s consider another insight: How does this representation differ for directed and undirected graphs? In a directed graph, every edge is unidirectional. So, for any directed edge (u, v), node v will only appear in the adjacency list of vertex u. On the other hand, in an undirected graph, every edge is bidirectional, i.e., if (u, v) is an undirected edge, then u appears in v’s adjacency list, and vice versa. So, what can be derived from this observation?

In a directed graph, the sum of the lengths of all the adjacency lists is equal to the number of edges.
In an undirected graph, the sum of the lengths of all the adjacency lists is equal to twice the number of edges.
In the adjacency-list representation of both directed and undirected graphs, the overall space complexity to represent the graph G(V, E) = O(V) + O(E) = O(V + E).

We can also use adjacency lists to represent weighted graphs. For example, in a directed graph, we can simply store the weight w(u, v) of the edge (u, v) in vertex v within the adjacency list of vertex u. Overall, the adjacency-list representation is quite flexible, allowing us to modify it to implement various types of graphs.

Adjacency list and adjacency representation example (directed and undirected graph)

Adjacency Matrix Representation of Graph

For the adjacency-matrix representation of a graph G = (V, E), we assume that the vertices are numbered from 1, 2, …, V. So, the adjacency-matrix representation of a graph G consists of a V x V matrix A, such that A[u][v] = 1 if there is an edge between u and v, and A[u][v] = 0 if there is no edge between u and v.

Here are some observations:

The adjacency matrix requires O(V²) memory, independent of the number of edges in the graph.
In an undirected graph, since (u, v) and (v, u) represent the same edge, the adjacency matrix representation of the undirected graph is symmetrical along the main diagonal. So the adjacency matrix A of an undirected graph is its own transpose. Can we use this idea to optimize the space required to represent undirected graph? Think and explore.
It may use a large amount of space for graphs with many vertices and relatively few edges. Suppose there is a 20 x 25 street in your city. This will give you 500 vertices and 1,000 edges, as each vertex neighbours four other vertices, and each edge is shared between two vertices. So in this scenario, the adjacency matrix would have 500 × 500 = 25,000 cells, almost all of them empty!
We can also use an adjacency matrix to represent a weighted graph. For example, we can simply store the weight w(u, v) of the edge (u, v) in row u and column v of the adjacency matrix. If an edge does not exist, we can store a NIL value in its corresponding matrix entry.

Adjacency matrix vs Adjacency list

Now, the critical question is: When should we use an adjacency list, and when should we use an adjacency matrix? Selecting the right graph data structure can have a significant impact on performance. Let’s explore this critical comparison.

In an undirected graph with V vertices, the maximum possible number of edges that can exist is V * (V — 1) / 2, which is O(V²). Here, we are assuming that there are no self-loops or parallel edges. So, the choice between an adjacency list and an adjacency matrix depends on the density of the graph.

If the graph is sparse i.e. the number of edges E is much less than the number of vertices V, or E is close to V, we prefer an adjacency list because it will take O(V + E) memory. This helps us store only the existing edges in a memory-efficient manner. On the other hand, if we use an adjacency matrix for a sparse graph, it will unnecessarily use O(V²) space.
We prefer an adjacency-matrix representation when the graph is dense, i.e., the number of edges E is much larger than V, or when we need to quickly determine if there is an edge connecting two given vertices. On the other hand, the adjacency list provides no quicker way to determine whether a given edge (u, v) is present in the graph. For this, we need to traverse the length of the adjacency list of node u in the worst case.
Although the adjacency-list representation is asymptotically at least as space-efficient as the adjacency-matrix representation, adjacency matrices are simpler, and so we may prefer them when graphs are reasonably small. Moreover, adjacency matrices carry a further advantage for unweighted graphs: they require only one bit per entry.

Performance comparison of adjacency list and adjacency matrix representation of graph

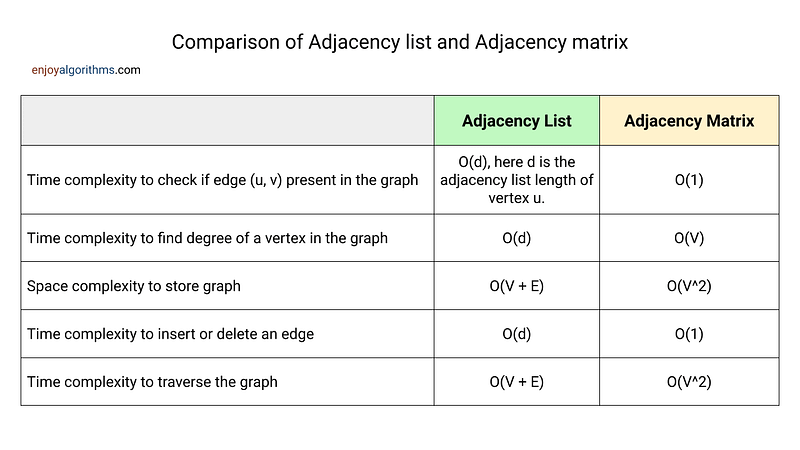
As we can see from the above table, adjacency lists make it harder to verify whether a given edge (u, v) exists, as we must search through the appropriate list to find the edge. However, it is easy to design graph algorithms that avoid the need for such queries. For example, we can explore all the edges of the graph in one pass via a breadth-first or depth-first traversal and perform operations on the current edge as we visit it. In this way, adjacency lists are the right data structure for most graph applications.

Basic Graph Operations

Adjacency list representation using vector or array list

In this code, the Graph class uses an adjacency list representation for the graph and supports various operations such as adding edges, deleting edges and storing information about the vertices and edges.

struct Edge 
{
    int destination;
    int weight;     
};

class Graph 
{
private:
    int V;
    // Flag to indicate if the graph is directed
    bool directed;
    // Vector of vectors to represent adjacency list for each vertex.
    vector<vector<Edge>> adj;
    // Store the degree of each vertex.
    vector<int> degree;

public:
    // Constructor for the Graph class
    Graph(int vertices, bool isDirected) 
    {
        V = vertices;
        directed = isDirected;
        adj.resize(V);
        degree.resize(V, 0);
    }
    
    // Function to add an edge with weight
    void addEdge(int u, int v, int weight) 
    {
        Edge edge1 = {v, weight};
        adj[u].push_back(edge1);
        degree[u] = degree[u] + 1;
        
        if (directed == false) 
        {
            Edge edge2 = {u, weight};
            // Add the reverse edge for an undirected graph
            adj[v].push_back(edge2);
            degree[v] = degree[v] + 1;
        }
    }
    
    // Function to delete an edge
    void deleteEdge(int u, int v) 
    {
        // Search for the edge in the adjacency list of u and remove it
        for (auto it = adj[u].begin(); it != adj[u].end(); ++it) 
        {
            if (it->destination == v) 
            {
                adj[u].erase(it);
                degree[u] = degree[u] - 1;
                break;
            }
        }
        
        // If the graph is undirected, also search and remove 
        // the reverse edge in the adjacency list of v. 
        if (directed == false) 
        {
            for (auto it = adj[v].begin(); it != adj[v].end(); ++it) 
            {
                if (it->destination == u) 
                {
                    adj[v].erase(it);
                    degree[v] = degree[v] - 1;
                    break;
                }
            }
        }
    }
    
    // Add other graph operations and algorithm here
};

Adjacency list representation using linked list

// Node to represent an edge
struct Node 
{
    int destination;  // Destination vertex
    int weight;       // Weight of the edge
    Node* next;       // Pointer to the next edge
    
    // Constructor to initialize a Node
    Node(int dest, int w)
    {
        destination = dest;
        weight = w;
        next = NULL;
    }
};

// Graph class with linked list representation
class Graph 
{
private:
    int V;           // Number of vertices
    bool directed;   // Indicates whether the graph is directed or undirected
    Node** adj;      // Array of pointers to linked lists representing the adjacency list
    int* degree;     // Array to store the degree of each vertex in the graph

public:
    // Constructor to initialize the graph
    Graph(int vertices, bool isDirected)
    {
        V = vertices;
        directed = isDirected;
        
        // Allocate memory for adjacency list and degree arrays
        adj = new Node*[V];
        degree = new int[V];
        
        // Initialize each vertex's adjacency list to NULL and degree to 0
        for (int i = 0; i < V; i++) 
        {
            adj[i] = NULL;
            degree[i] = 0;
        }
    }
    
    // Function to add an edge to the graph
    void addEdge(int u, int v, int weight) 
    {
        // Create an edge from u to v with the given weight
        Node* newNode = new Node(v, weight);
        
        // Add the new edge to the beginning of u's adjacency list
        newNode->next = adj[u];
        adj[u] = newNode;
        
        // Increase the degree of vertex u
        degree[u] = degree[u] + 1;
        
        if (directed == false) 
        {
            // If the graph is undirected, add the reverse edge from v to u
            newNode = new Node(u, weight);
            
            // Add the reverse edge to the beginning of v's adjacency list
            newNode->next = adj[v];
            adj[v] = newNode;
            
            // Increase the degree of vertex v as well
            degree[v] = degree[v] + 1;
        }
    }
    
    // Function to delete an edge from the graph
    void deleteEdge(int u, int v) 
    {
        Node* current = adj[u];
        Node* prev = NULL;
        
        // Search for the edge from u to v in the adjacency list of u
        while (current != NULL && current->destination != v) 
        {
            prev = current;
            current = current->next;
        }
        
        // If the edge is not found, return
        if (current == NULL)
            return;
        
        // If the edge is found, remove it from the linked list
        if (prev != NULL)
            prev->next = current->next;
        else
            adj[u] = current->next;
        
        // Delete the removed edge's memory
        delete current;
        
        // Decrease the degree of vertex u
        degree[u] = degree[u] - 1;
        
        if (directed == false) 
        {
            // If the graph is undirected, repeat the process for the reverse edge from v to u
            current = adj[v];
            prev = NULL;
            while (current != NULL && current->destination != u) 
            {
                prev = current;
                current = current->next;
            }
            
            if (current == NULL)
                return;
            
            if (prev != NULL)
                prev->next = current->next;
            else
                adj[v] = current->next;
            
            delete current;
            
            degree[v] = degree[v] - 1;
        }
    }
    
    // Add other graph operations and algorithms here
};

Adjacency matrix representation

class Graph 
{
private:
    int V;              
    bool directed;    
    // 2D vector to represent the adjacency matrix of the graph, 
    // which stores the edge weights between vertices.
    vector<vector<int>> adjMatrix;
    // Vector to store the degree of each vertex
    vector<int> degree;

public:
    // Constructor to initialize the graph
    Graph(int vertices, bool isDirected)
    {
        V = vertices;
        directed = isDirected;    
        // Initialize the adjacency matrix with zeros (no edges)
        adjMatrix.resize(V, vector<int>(V, 0));  
        // Initialize the degree vector with zeros (no edges)
        degree.resize(V, 0);
    }
    
    // Function to add an edge to the graph
    void addEdge(int u, int v, int weight) 
    {
        // Set the edge weight in the adjacency matrix from u to v
        adjMatrix[u][v] = weight;    
        // Increase the degree of vertex u
        degree[u] = degree[u] + 1; 
        if (directed == false)
        {
            // If the graph is undirected, set the edge weight from v to u
            adjMatrix[v][u] = weight;       
            // Increase the degree of vertex v as well
            degree[v] = degree[v] - 1;
        }
    }
    
    // Function to delete an edge from the graph
    void deleteEdge(int u, int v) 
    {
        // Remove the edge by setting the edge weight to 0 from u to v
        adjMatrix[u][v] = 0;  
        // Decrease the degree of vertex u
        degree[u] = degree[u] - 1;
        
        if (directed == false) 
        {
            // If the graph is undirected, remove the edge from v to u as well
            adjMatrix[v][u] = 0;      
            // Decrease the degree of vertex v as well
            degree[v] = degree[v] - 1;
        }
    }
    
    // You can add other graph operations and algorithms here
};

Critical idea to think!

Is there another way to represent a graph?
Which graph algorithms work perfectly with an adjacency list?
Which graph algorithms work perfectly with an adjacency matrix?
The adjacency matrix representation of an undirected graph is symmetrical in terms of the matrix diagonal. Can we use this idea to optimize space?
Apart from degree and weight, what other types of additional information can we store inside the edges or nodes of a graph?

Enjoy learning, enjoy algorithms!

Adjacency List and Adjacency Matrix Representation of Graph