Heapify Operation on Heap Data Structure

We use the heapify operation to fix the violation of heap property at a given node in the heap. Such violations actually happen due to several reasons: 1) After inserting a new element in the heap 2) After removing the max element in a max heap or min element in the max heap 3) After updating some value with the new value.

The idea of the heapify process is similar for both max and min heap: We need to reverse the order of comparison in the code! So here we will discuss the idea of heapify procedure using the max heap.

Depending on the types of heap property violation at any node, there are two types of heapify operation: 1) Top-down heapify 2) Bottom-up heapify. Understanding these two process are critical for implementing several heap operations like heap building from an array, insertion on a heap, etc.

Top-down Heapify Operation

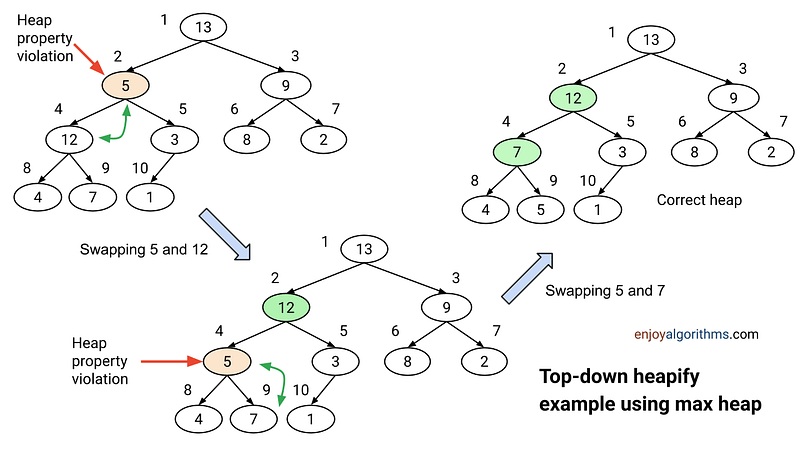
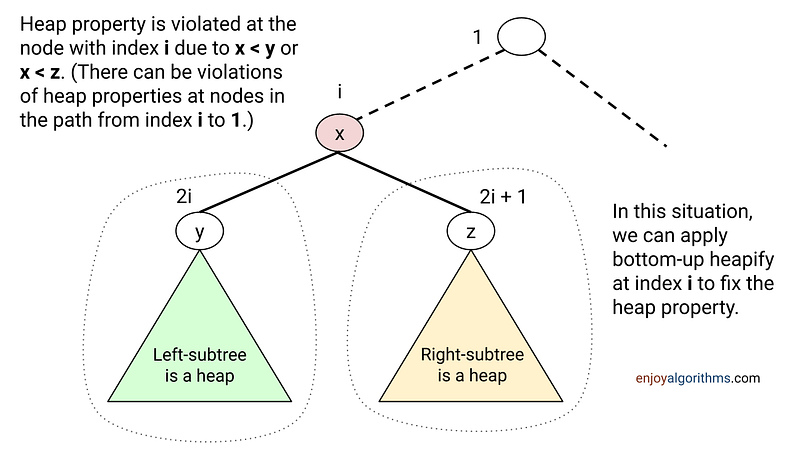
Suppose there is a violation of the max heap property at a node with index i. It means the value stored at index i is less than the value stored at one or both of its children (at index 2i and 2i + 1) and the binary tree rooted at both children is the max heap. So to maintain the max-heap property at index i, we use a top-down heapify process. Let’s discuss this idea in detail!

Solution idea

Based on the max heap property, the value at index i must be greater than the value at both children. So one idea to fix the violation is to update the value at index i with the maximum of its children value. In other words, we can make progress toward fixing the violation by swapping the value at index i with the larger of its two children.

But this swap may cause a violation of heap property at the child node. So we proceed in the same way and call the heapify procedure recursively for the child node. So we move down the heap until we reach a node with both children smaller (or equal), or the bottom.

Solution code C++

void topDownHeapify(vector<int>& heap, int heapSize, int i) 
{
    int largest = i;  // Initialize largest as root
    int left = 2 * i + 1;  // Left child
    int right = 2 * i + 2; // Right child

    // If left child is larger than root
    if (left < heapSize && heap[left] > heap[largest])
        largest = left;

    // If right child is larger than largest so far
    if (right < heapSize && heap[right] > heap[largest])
        largest = right;

    // If the largest is not the root, swap root with the largest
    if (largest != i) 
    {
        swap(heap[i], heap[largest]);

        // Recursively heapify the affected sub-tree
        maxHeapify(heap, heapSize, largest);
    }
}

Solution code Python

def top_down_heapify(heap, heap_size, i):
    largest = i  # Initialize largest as root
    left = 2 * i + 1  # Left child
    right = 2 * i + 2  # Right child

    # If left child is larger than root
    if left < heap_size and heap[left] > heap[largest]:
        largest = left

    # If right child is larger than largest so far
    if right < heap_size and heap[right] > heap[largest]:
        largest = right

    # If the largest is not the root, swap root with the largest
    if largest != i:
        heap[i], heap[largest] = heap[largest], heap[i]

        # Recursively heapify the affected sub-tree
        top_down_heapify(heap, heap_size, largest)

Time complexity analysis

Heap property is violated at the sub-heap rooted at index i and we move down the tree. So in the worst case, we will traverse the height of the sub-heap rooted at index i. So what would be its height? Height of sub-heap rooted at index i = Height of the heap — Distance of node at index i from the root = log(n) — log (i).

So the extreme worst-case scenario will occur when there is a violation of heap property at the root node (index 1) and we need to traverse the complete logn height from the root to one of the leaf nodes to fix the heap property violation. So worst case time complexity will be O(logn).

There is one more observation: The height of most of the sub-heaps will be very small because n/2 nodes are a heap of height 0 (leaf nodes), n/4 nodes are a heap of height 1, n/8 nodes are a heap of height 2, and so on. So time complexity of the top-down heapify operation for all the nodes closer to leaf nodes will be constant! Awesome!

That’s why we use this insight to build max-heap in a bottom-up manner with O(n) time complexity even if it looks O(nlogn) at first sight! We also use top-down heapify in the deleteMax operation.

Bottom-up Heapify Operation

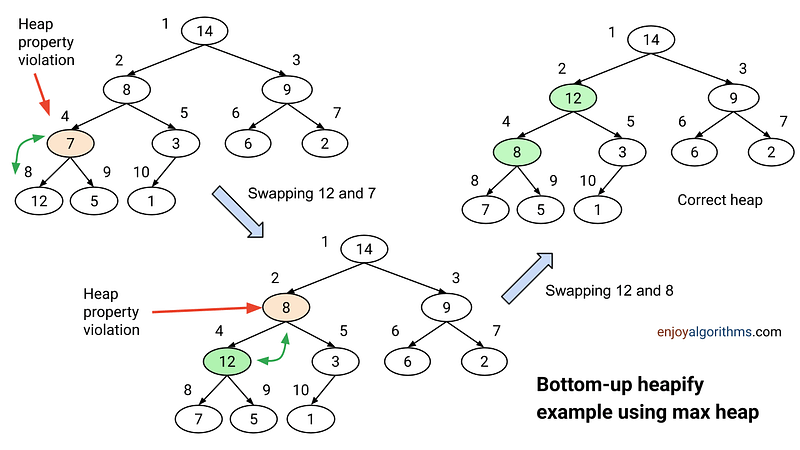
Now consider another scenario! Suppose the heap property is violated because the value of the node at index i becomes larger than the value of its parent node (at index i/2). How can fix this? The idea would be the same as above but we need to move in the opposite direction i.e. path from node at index i to root node at index 1 (In the worst case, we have to traverse till root node). Let’s understand this in detail!

Solution idea

We can make progress toward fixing the violation by swapping the node value with the value at its parent node. After this swap, now value at the parent node will be larger than both its children (one is the old parent, and the other is smaller than the old parent because it was a child of that node).

But again just like the top-down heapify, the value at the parent node may still be larger than its parent. So, we can fix this violation by moving up the heap until we reach a node with a larger key or the root.

Solution code C++

void bottomUpHeapify(vector<int>& heap, int i) 
{
    // Loop while the current element is greater than its parent
    while (i > 1 && heap[i] > heap[i/ 2]) 
    {
        // Swap the current element with its parent
        swap(heap[i], heap[i/2]);
        // Move to the parent index
        i = i/ 2;
    }
}

Solution code Python

def bottom_up_heapify(heap, i):
    # Loop while the current element is greater than its parent
    while i > 0 and heap[i] > heap[i // 2]:
        # Swap the current element with its parent
        heap[i], heap[i // 2] = heap[i // 2], heap[i]
        
        # Move to the parent index
        i = i // 2

Time complexity analysis

We are moving up the tree from index i to root node in the worst case. So the total distance travelled in the worst case = Distance of node at index i from the root node at index 1 = log (i).

So the extreme worst-case scenario will occur when there is a violation of heap property at some leaf node (from index n/2 + 1 to n) and we need to traverse the complete logn height from the leaf node to the root node to fix the violation. So worst case time complexity will be O(logn).

• There is again an observation: For a large number of nodes (leaf nodes or nodes closer to leaf nodes), the time complexity will be closer to the worst case i.e. O(logn). On the other side, only a small number of nodes closer to the root node will have time complexity closer to the best case.
• We use bottom-up heapify to build a heap in a top-down manner, insert a new element in the heap and perform an increase key operation in the max heap.

We will keep adding more insights to this blog. Enjoy learning, enjoy algorithms! If you have some queries or feedback, please share in the message below!