Implement Least Recently Used (LRU) Cache
Difficulty: Hard, Asked-in: Amazon, Microsoft, Adobe, Google.
Key takeaway: an excellent algorithm to learn data structure design and problem-solving using hash tables and doubly-linked lists.
Understanding LRU cache problem
The Least Recently Used (LRU) cache is a popular caching strategy that discards the least recently used items first to make room for new elements when the cache is full. It organizes items in the order of their use, allowing us to easily identify items that have not been used for a long time. This strategy is useful for optimizing the use of limited cache space and improving the performance of caching systems.
So our goal is to design a data structure that follows the constraints of a Least Recently Used (LRU) cache. We need to implement LRUCache class with the following operations:
- LRUCache(int capacity): Initialize LRU cache with positive size capacity.
- int get(int key): Return the value of key if key exists, otherwise, return -1.
- void put(int key, int value): Update the value of key if key exists. Otherwise, add key-value pair to the cache. If number of keys exceeds the capacity of lru cache, evict the least recently used key.
We want the following specifications from our LRU cache:
- Access time for any item should be O(1).
- Time required to get the least recently used element should be O(1).
- Time required to put any item should be O(1).
- The space required should be O(n).
Let's understand the problem via an example
Suppose we have five elements in the main memory, A1 to A5. And let the size of our cache be 3.
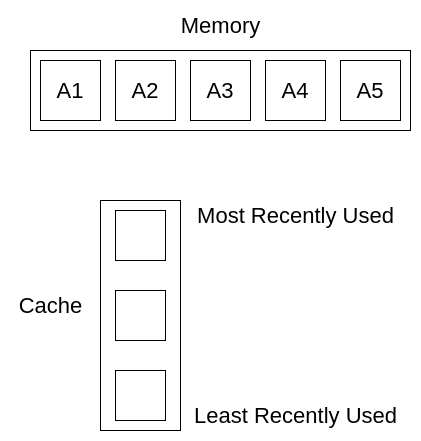
Initially, the cache is empty, and all the elements are stored in memory. We want to get A1 first. We get the value of A1 from memory and store it in the cache.
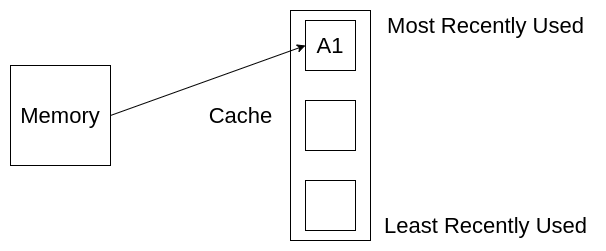
Next, we want to get A2. A2 gets stored at the topmost level, and A1 is moved down as it is no longer the most recently used element.
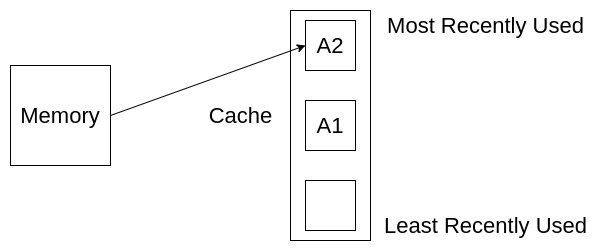
Next, we want to get A3.
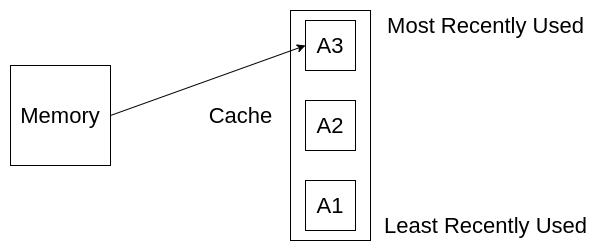
Now suppose we want to get A2 again. Instead of getting this from memory, we can get this from our cache. Notice that the position of A2 is at the top again, as A2 is the most recently used element now.
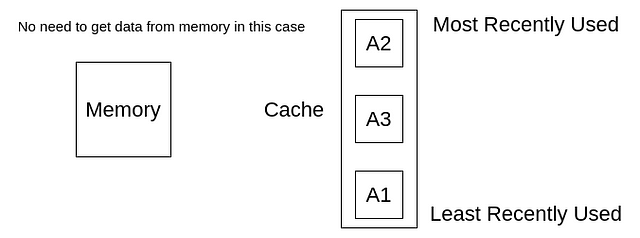
Now we want to get A4. We have to get it from memory. But where will we store it in our cache? We have to remove some elements so that we can keep A4. So, we remove the least recently used element, A1, in this case.
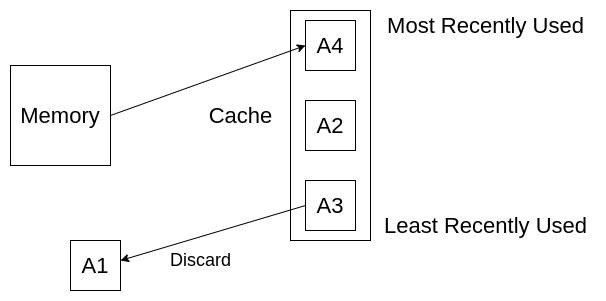
Since our cache can store only three elements, we need to discard the least recently used element from our cache.
Before designing the implementation of the LRU cache, we will look at the need for a cache. Generally, retrieving data from a computer’s memory is an expensive task. A high-speed memory known as cache memory is used to avoid accessing data from memory repeatedly. A cache holds frequently requested data and instructions to be immediately available to the CPU. Thus, cache memory reduces the average time for accessing data from the main memory.
The cache memory size is generally much smaller than the main memory. So we cannot fit everything from the main memory into the cache. There are different ways of handling this; LRU cache is one such way. The main idea of the LRU cache is to store the n recently accessed elements (assume that the size of the cache is n).
Brute force approach: LRU cache using simple array
We initialize an array of sizes equal to that of our cache. Here each data element stores extra information to mark with an access time stamp. It shows the time at which the key is stored. We will use the timeStamp to find out the least recently used element in the LRU) cache.
class DataElement {
int key;
int value;
int timeStamp;
public DataElement(int k, int data, int time) {
key = k;
value = data;
timeStamp = time;
}
}int get(int key): We need to traverse the array and search for the data element with the desired key. If the element is found, we set its timestamp to 0 and return its value. If the element is not found, we return -1. The time complexity for this operation is O(n), as we may need to traverse the entire array to find the desired element.
void put(int key, int value): If the array is not full, we insert the new data element by increasing the timestamp of the existing elements by 1, setting the timestamp of the new element to 0, and inserting it into the array. However, if the array is full and we need to make room for the new element, we must delete the least recently used element or the element with the largest timestamp. To do this, we iterate through the array and find the element with the largest timestamp. Then, we replace it with the new element and insert it into the array. The time complexity for this operation is O(n), as we may need to traverse the entire array to find the element with the largest timestamp.
Brute force approach: LRU cache using singly linked list
int get(int key): To retrieve a value from the LRU cache implemented with a linked list, we need to traverse the list and search for the data element with the desired key. If it is found, we move the element to the head of the list and return its value. If the element is not found, we return -1. The time complexity for this operation is O(n), as we may need to traverse the entire linked list to find the desired element.
void put(int key, int value): If the length of the linked list is less than the size of the cache, we simply insert the new data element at the head of the list. However, if the cache is full, we need to delete the least recently used element, which is located at the tail of the linked list. To do this, we must traverse the linked list until we reach the end, resulting in a worst-case time complexity of O(n).
The critical question is: the time complexity of both get and put operations in both approaches is O(n), which is inefficient and does not satisfy the specification given in the problem. It's an exercise for you to write the implementation code for both approaches!
Efficient approach using hash map and doubly linked list
Solution idea
To implement a Least Recently Used (LRU) cache that meets our requirements, we need to use a combination of a doubly-linked list and a hash map. The doubly-linked list allows us to store the elements in a specific order (with the least recently used element at the bottom) and move any element to the top in constant time. However, accessing an element in the doubly-linked list would take O(n) time. To address this, we use a hash map to map the elements to doubly-linked list nodes, allowing us to access an element in the doubly-linked list in O(1) time.
When inserting new data into the cache, we insert it into the head of the linked list and record it in the map. After each cache hit, we move the accessed data (nodes) to the head of the linked list. When the linked list is full, we discard the tail of the linked list and delete the corresponding map key to make room for the new element.
Solution steps
To access and update an element in the LRU cache implemented with a doubly-linked list and a hash map, we need to follow these steps:
- Look up the element in hash map.
- If the element is present in the hash map, it is stored in our cache and we do not need to retrieve it from memory (This is known as a cache hit). To mark the element as the most recently used, we retrieve its corresponding linked list node from the hash map and move it to the top of the list.
- If the element is not present in the hash map, it is not stored in our cache and we need to retrieve its value from memory. This is known as a cache miss.
- To make room for the new element, we may need to remove the least recently used element from the cache. This will be the last node of the linked list.
- We delete this element by removing the last node from the linked list and removing it from the hash map.
- Then, we create a new node for the element and insert it at the top of the cache (i.e. the head of the linked list).
- We also record the element in the hash map.
If we follow all these steps, we can update our cache in O(1) time as all these steps take O(1) time. Following is the implementation code of the LRU-cache.
LRU Cache Java Implementation
import java.util.Hashtable;
public class LRUCache {
class Node {
int key;
int value;
Node pre;
Node post;
}
private Hashtable<Integer, Node> cache = new Hashtable<Integer, Node>();
private int count;
private int capacity;
private Node head, tail;
// Add the new node right after head
private void addNode(Node node) {
node.pre = head;
node.post = head.post;
head.post.pre = node;
head.post = node;
}
// Remove an existing node from the linked list
private void removeNode(Node node) {
Node pre = node.pre;
Node post = node.post;
pre.post = post;
post.pre = pre;
}
// Move node in between to the head
private void moveToHead(Node node) {
removeNode(node);
addNode(node);
}
// Pop the current tail
private Node popTail() {
Node res = tail.pre;
removeNode(res);
return res;
}
public LRUCache(int capacity) {
this.count = 0;
this.capacity = capacity;
head = new Node();
head.pre = null;
tail = new Node();
tail.post = null;
head.post = tail;
tail.pre = head;
}
public int get(int key) {
Node node = cache.get(key);
if (node == null) {
return -1;
}
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
Node node = cache.get(key);
if (node == null) {
Node newNode = new Node();
newNode.key = key;
newNode.value = value;
cache.put(key, newNode);
addNode(newNode);
++count;
if (count > capacity) {
// Pop the tail
Node tailNode = popTail();
cache.remove(tailNode.key);
--count;
}
} else {
// Update the value.
node.value = value;
moveToHead(node);
}
}
}LRU Cache Python Implementation
class Node:
def __init__(self, k, v):
self.key = k
self.val = v
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity):
self.capacity = capacity
self.hashMap = dict()
self.head = Node("#", 0)
self.tail = Node("-", 0)
self.head.next = self.tail
self.tail.prev = self.head
def get(self, key):
if key in self.hashMap:
node = self.hashMap[key]
self._remove(node)
self._add(node)
return node.val
return -1
def put(self, key, value):
if key in self.hashMap:
self._remove(self.hashMap[key])
newNode = Node(key, value)
self._add(newNode)
self.hashMap[key] = newNode
if len(self.hashMap) > self.capacity:
nodeToRemove = self.tail.prev
self._remove(nodeToRemove)
del self.hashMap[nodeToRemove.key]
def remove_node(self, node):
previousNode = node.prev
nextNode = node.next
previousNode.next = nextNode
nextNode.prev = previousNode
def add_node(self, node):
nextNode = self.head.next
previousNode = self.head
previousNode.next = node
nextNode.prev = node
node.next = nextNode
node.prev = previousNodeLRU Cache C++ Implementation
#include <unordered_map>
class LRUCache {
private:
struct Node {
int key;
int value;
Node* pre;
Node* post;
};
unordered_map<int, Node*> cache;
int count;
int capacity;
Node* head;
Node* tail;
// Add the new node right after head
void addNode(Node* node) {
node->pre = head;
node->post = head->post;
head->post->pre = node;
head->post = node;
}
// Remove an existing node from the linked list
void removeNode(Node* node) {
Node* pre = node->pre;
Node* post = node->post;
pre->post = post;
post->pre = pre;
}
// Move node in between to the head
void moveToHead(Node* node) {
removeNode(node);
addNode(node);
}
// Pop the current tail
Node* popTail() {
Node* res = tail->pre;
removeNode(res);
return res;
}
public:
LRUCache(int capacity) {
this->count = 0;
this->capacity = capacity;
head = new Node();
head->pre = nullptr;
tail = new Node();
tail->post = nullptr;
head->post = tail;
tail->pre = head;
}
int get(int key) {
if (cache.find(key) == cache.end()) {
return -1;
}
Node* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (cache.find(key) == cache.end()) {
Node* newNode = new Node();
newNode->key = key;
newNode->value = value;
cache[key] = newNode;
addNode(newNode);
++count;
if (count > capacity) {
// Pop the tail
Node* tailNode = popTail();
cache.erase(tailNode->key);
--count;
}
}
else {
// Update the value.
Node* node = cache[key];
node->value = value;
moveToHead(node);
}
}
};The Least Recently Used (LRU) cache has several advantages and disadvantages:
Advantages:
- Fast access: The cache stores items in the order of most recently used to least recently used, allowing us to access both the least recently used element and the most recently used element in O(1) time.
- Fast updates: We can find any element in the cache in O(1) time, so updating the cache also takes O(1) time.
Disadvantages:
- Space complexity: To implement the LRU cache, we need to use both a linked list and a hash map, each of which takes O(n) space.
Similar coding questions to practice
- Design LFU Cache
- Design Bloom Filter
- Design Min Stack
- Design add and search words data structure
Enjoy learning! Enjoy coding!