Find Minimum in a Rotated and Sorted Array

Difficulty: Medium, Asked-In: Facebook, Amazon, Microsoft, Adobe, Morgan Stanley

Key takeaway: An excellent problem to learn problem-solving using binary search.

Let’s understand the problem

A sorted and rotated array of size n is given. Write a program to find the minimum element in this sorted and rotated array.

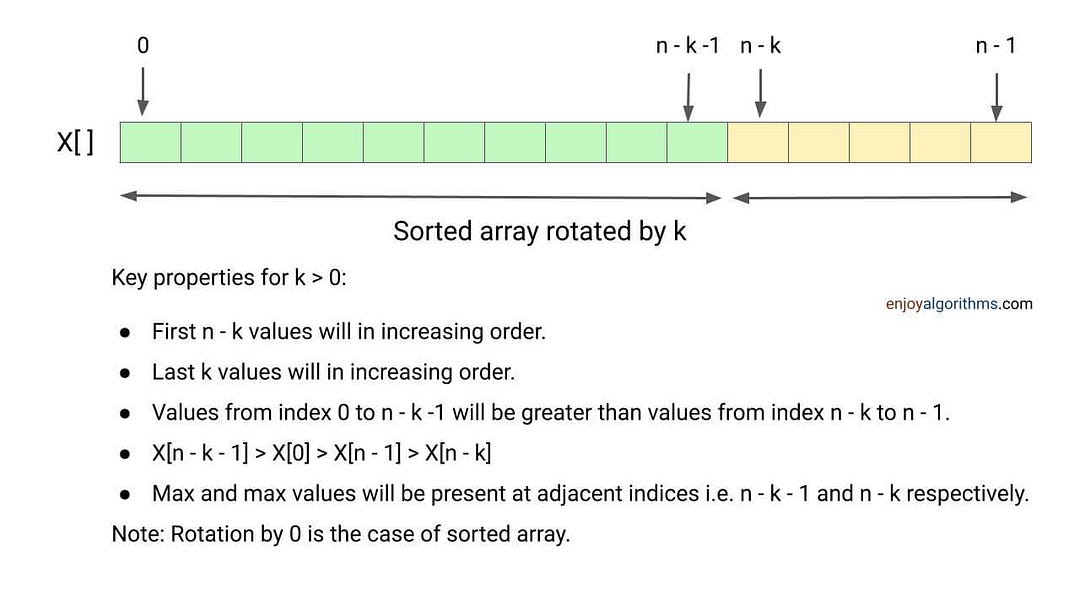
Rotation by k means: The first k elements of the array will move to the last k positions, and the last n - k elements will move to the first n - k positions (in an anti-clockwise fashion). For example, rotating an array X[0], X[1], X[2], ..., X[n-1] three-time results in the array X[3], X[4], X[5], ..., X[n-2], X[n-1], X[0], X[1], X[2].

• We don’t know how many times array is rotated in the given problem.
• Assume that all elements in the array are unique.

Example 1

Input: X[] = [5, 6, 7, 8, 9, 1, 2, 3, 4], Output: 1

Explanation: Array is rotated by 4, so minimum element is present at index 5. 

Example 2

Input: X[] = [8, 9, 3, 4, 5, 6, 7], Output: 3

Explanation: Array is rotated by 5, so minimum element is present at index 2.

Example 3

Input: X[] = [5, 6, 7, 8, 9], Output: 5

Explanation: Array is not rotated at all, so minimum element is present at index 0.

Example 4

Input: X[] = [8, 7], Output: 7

Explanation: Array is not rotated by 1, so minimum element is present at index 1.

Discussed solution approaches

• A brute force approach using linear search
• An efficient approach using binary search 

A brute force approach using linear search

One basic idea would be to traverse array from start to end and find the minimum element. For this, we initialize a variable minRotated to track the minimum. Whenever we find a value X[i] less than minRotated, we update the minRotated with the X[i]. By the end of loop, the minimum value gets stored in variable minRotated.

Solution pseudocode

int minRotatedArray(int X[], int n)
{
    int minRoated = X[0]
    for (int i = 1; i < n; i = i + 1)
    { 
        if(minRotated > X[i])
            minRotated = X[i]    
    }
    return minRotated
}

Solution analysis

We traverse the array using a single loop and perform constant operations at each iteration. So time complexity = O(n). We use constant extra space, so space complexity = O(1).

An efficient approach using binary search

Now the critical question is: Can we think to improve the time complexity using the property of sorted and rotated array? Is there some insight that can help us to reduce the comparison operations? One idea looks obvious: Input array is almost similar to sorted array, and we need to search for something. Can we think of applying a binary search approach?

Solution idea

If we look closely, we can recognize three cases:

• Case 1: When the leftmost value is less than the rightmost value, the minimum element will be present at the leftmost index. In other words, array is not rotated at all and we return the leftmost value.
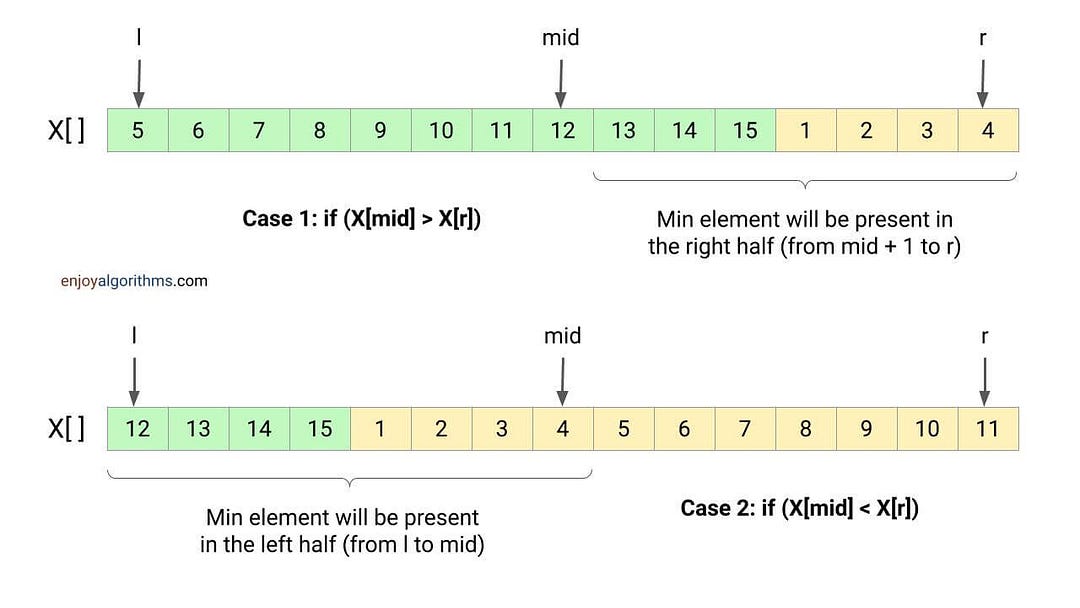
• Case 2: When the value at the mid-index is greater than the rightmost value, the minimum element will be present on the right half. 
• Case 3: When the value at the mid-index is less than the rightmost value, then the minimum element will be present on the left half.

So we can think of applying a modified version of binary search where case 2 and case 3 decides the search direction.

Iterative solution

Implementation steps

We initialize two variables l and r with 0 and n - 1. Now we run a loop till l < r.

• If (X[l] < X[r]), return X[l].
• Now we calculate the mid index i.e. mid = l + (r  -  l)/2
• If (X[mid] > X[r]), we search the minimum in the right half. For this, we update l = mid + 1.
• Otherwise, we search in the left half. For this, we update r = mid.

By the end of loop, we return X[l] as an minimum.

Implementation code C++

int minRotatedArray(int X[], int n)
{
    int l = 0;
    int r = n - 1;
    while (l < r) 
    {
        if (X[l] < X[r])
            return X[l];
        int mid = l + (r - l)/2;
        if (X[mid] > X[r])
            l = mid + 1;  
        else
            r = mid;      
    }
    return X[l];
}

Implementation code Python

def minRotatedArray(X, n):
    l = 0
    r = n - 1
    while l < r:
        if X[l] < X[r]:
            return X[l]
        mid = l + (r - l)//2
        if X[mid] > X[r]:
            l = mid + 1
        else:
            r = mid
    return X[l]

Recursive solution

Implementation steps

We define a function minRotated(int X[], int l, int r), where parameters l and r are initialized with 0 and n  -  1.

• If (X[l] < X[r]), we return X[l].
• We calculate the mid index i.e. mid = l + (r  -  l)/2
• If (X[mid] > X[r]), we search minimum in the right half. For this, we call the same function with updated left parameter l equal to mid + 1 i.e. minRotatedArray(X, mid + 1, r). 
• Otherwise, we search minimum in the left half. For this, we call the same function with updated right parameter r equal to mid i.e. minRotatedArray(X, l, mid).

Implementation code C++

int minRotatedArray(int X[], int l, int r)
{
    if(l < r)
    {
        if (X[l] < X[r])      
            return X[l];
        int mid = l + (r - l)/2;
        if (X[mid] > X[r])
            return minRotatedArray(X, mid + 1, r);
        else 
            return minRotatedArray(X, l, mid);
    }
    return X[l];
}

Implementation code Python

def minRotatedArray(X, l, r):
    if l < r:
        if X[l] < X[r]:      
            return X[l]
        mid = l + (r - l)//2
        if X[mid] > X[r]:
            return minRotatedArray(X, mid + 1, r)
        else:
            return minRotatedArray(X, l, mid)
    return X[l]

Solution analysis

At each step of iteration or recursion, we are decreasing the input size by half. In other words, the time complexity of the above approach is equal to the time complexity of binary search. Time complexity = O(log n).

• The space complexity of iterative solution = O(1)
• The space complexity of recursive solution = O(logn) for the call stack. 

Critical ideas to think about!

• Why are we returning X[l] after the end? Is it necessary?
• Does the above approach work fine if we have duplicates?
• Can we think of other different approaches to solve this problem?
• Is this operation necessary inside the loop: if(X[l] < X[r]), return X[l]? Does the above approach work fine if we put this condition before the loop?
• Can we keep the loop condition l ≤ r instead of l < r?
• In a rotated array, elements before and after the min element are greater than the min element. Can we think of applying binary search differently by comparing the adjacent elements of the mid-index?
• Instead of comparing X[mid] with X[r], can we think of solving this problem by comparing X[mid] and X[l]?
• Why do we need to include X[mid] when we are going in the left half? What will happen if we set r = mid - 1?

Similar problems to practice

• Search in rotated sorted array
• Find the first or last occurrence of a given number in a sorted array
• Find the maximum in an array which is first increasing and then decreasing

Enjoy learning, Enjoy algorithms!