Time Series Data Pre-processing in Machine Learning

Time series data is found everywhere, and to perform the time series analysis, we must preprocess the data first. Time Series preprocessing techniques have a significant influence on data modeling accuracy. 

Key takeaways from this blog

In this article, we will be discussing mainly these points:

1. Definition of time-series data and its importance.
2. Preprocessing steps for time series data.
3. Structuring time-series data, finding the missing values, denoising the features, and finding the outliers present in the dataset.

To begin with, let’s understand the definition of time series first:

Time Series is a sequence of evenly spaced observations recorded at a specific time interval. 

An example of time series would be the gold prices. In this case, our observation is the gold price collected over a while after fixed time intervals. The time unit could be in minutes, hours, days, years, etc. But the time difference between any two consecutive samples will be the same.

In this article, we will see the common time-series preprocessing steps that should be carried out before diving into the data modeling part. Let’s look at the common problems associated with the time-series data.

Preprocessing Time Series Data

Time Series data holds a lot of information, but generally, it is not visible. The common problems associated with time series are un-ordered timestamps, missing values (or timestamps), outliers, and noise in the data. Of all the mentioned problems, handling the missing values is the most difficult one. Since the conventional imputation (A technique used to take care of the missing data by replacing the missing values to retain most of the information) methods are not applicable while working with the time series data. To analyze the real-time analysis of this preprocessing, we will use Kaggle’s Air Passenger dataset, which can be downloaded from here.

Structuring Time Series 

Time Series data is generally found in unstructured formats, i.e., Timestamps could be mixed and not properly ordered. Also, most of the time, the date-time column has default string data type, and it is essential to covert the data-time column to date-time datatype first before applying any operation to it. Let’s implement this into our dataset:

import pandas as pd
passenger = pd.read_csv('AirPassengers.csv')
passenger['Date'] = pd.to_datetime(passenger['Date']) 
passenger.sort_values(by=['Date'], inplace=True, ascending=True)
#Above line will sort the values according to dates.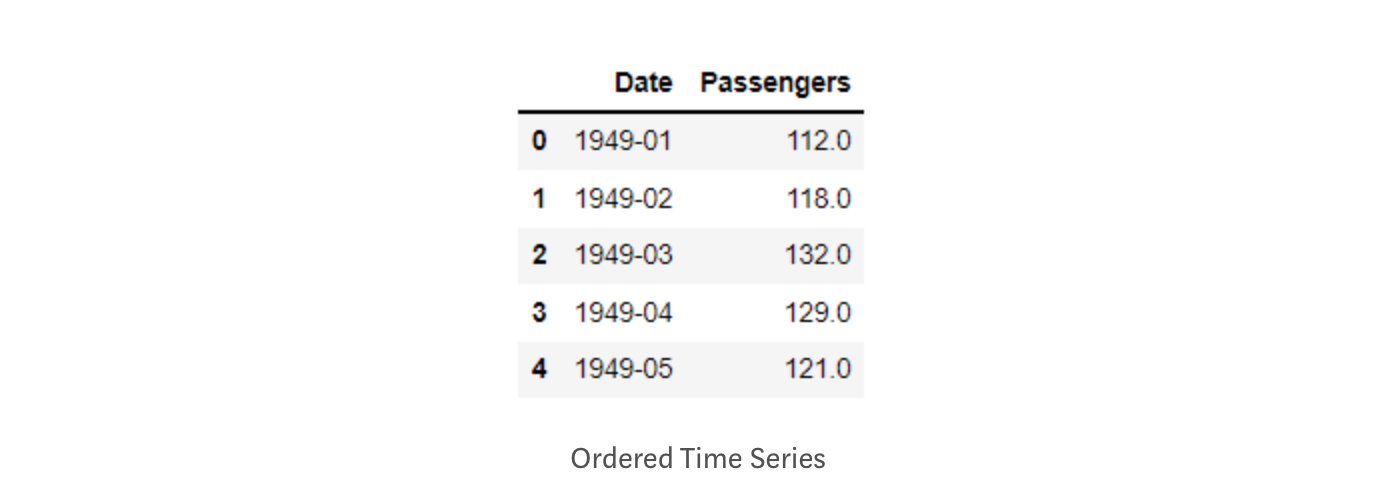

Missing Value Imputation in Time Series

Handling the missing values in time series data is a challenging task. Conventional imputation techniques are not applicable for the time-series data since the sequence in which values are received matters. To address this problem, we have the following Interpolation methods:

Interpolation 

Interpolation is a commonly used technique for time series missing value imputation. It helps in estimating the missing data-point using the two surrounding known data points. This method is simple and most intuitive. However, interpolation further has the following sub-methods: 

• Time-Based Interpolation 
• Spline Interpolation 
• Linear Interpolation 

Let’s see how our data looks like before imputation:

from matplotlib.pyplot import figure
import matplotlib.pyplot as plt
figure(figsize=(12, 5), dpi=80, linewidth=10)
plt.plot(passenger['Date'], passenger['Passengers'])
plt.title('Air Passengers Raw Data with Missing Values')
plt.xlabel('Years', fontsize=14)
plt.ylabel('Number of Passengers', fontsize=14)
plt.show()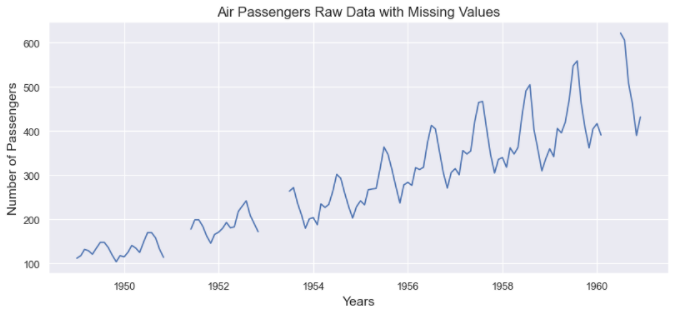

Before Imputation

Let’s take a look at the imputations:

passenger['Linear'] = passenger['Passengers'].interpolate(method='linear')
passenger['Spline order 3'] = passenger['Passengers'].interpolate(method='spline', order=3)
passenger['Time'] = passenger['Passengers'].interpolate(method='time')
methods = ['Linear', 'Spline order 3', 'Time']
from matplotlib.pyplot import figure
import matplotlib.pyplot as plt
for method in methods:
    figure(figsize=(12, 4), dpi=80, linewidth=10)
    plt.plot(passenger["Date"], passenger[method])
    plt.title('Air Passengers Imputation using: ' + types)
    plt.xlabel("Years", fontsize=14)
    plt.ylabel("Number of Passengers", fontsize=14)
    plt.show()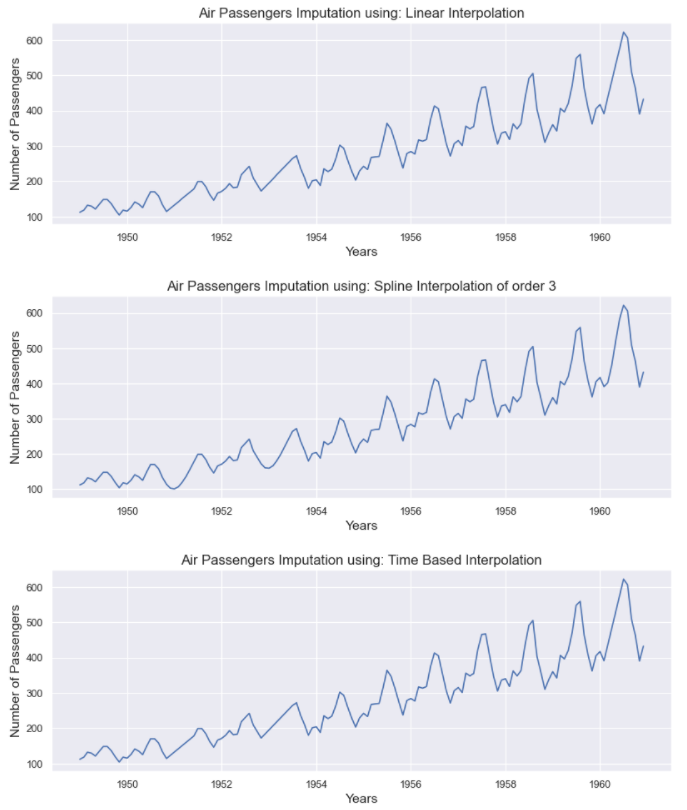

All methods have given a reliable set of imputations. Imputations from these methods make more sense when the missing value window ( width of missing data) is small. For instance, if several consecutive values are missing, it becomes harder for these methods to estimate them. 

Denoising a Time Series

Noise elements in a time series can cause significant problems, and noise removal is highly recommended before building any model. The process of carefully minimizing the noise is called denoising. Following are some methods commonly used for removing the noise from a time series:

• Rolling means

The Rolling mean is simply the mean for a window of previous observations, where the window is a sequence of values from the time series data. Mean is calculated for each ordered window. This can greatly help in minimizing the noise in time series data.  

Let’s apply the rolling mean on Google Stock Price:

rolling_google = google_stock_price['Open'].rolling(20).mean()
plt.plot(google_stock_price['Date'], google_stock_price['Open'])
plt.plot(google_stock_price['Date'], rolling_google)
plt.xlabel('Date')
plt.ylabel('Stock Price')
plt.legend(['Open','Rolling Mean'])
plt.show()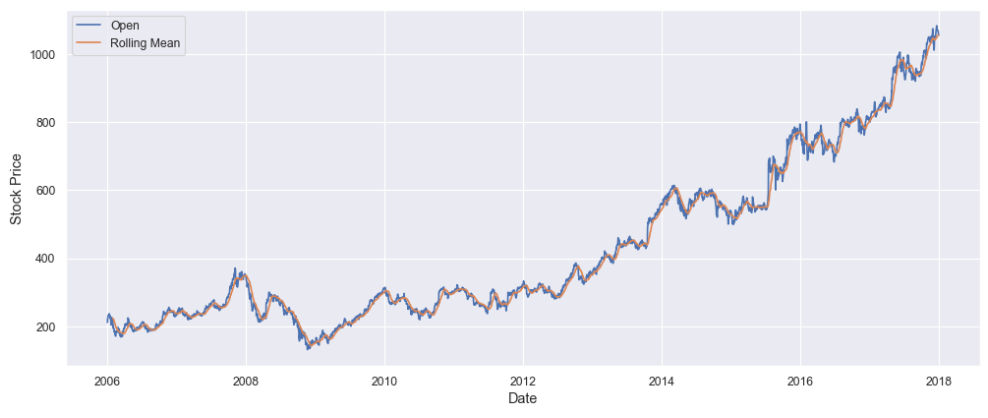

• Fourier Transform

Fourier Transform can help remove the noise by converting the time series data into the frequency domain, and from there, we can filter out the noisy frequencies. Then, we can apply the inverse Fourier transform to obtain the filtered time series. Let’s use Fourier transform on the Google Stock Price.

denoised_google_stock_price = fft_denoiser(value, 0.001, True)
plt.plot(time, google_stock['Open'][0:300])
plt.plot(time, denoised_google_stock_price)
plt.xlabel('Date', fontsize = 13)
plt.ylabel('Stock Price', fontsize = 13)
plt.legend(['Open','Denoised: 0.001'])
plt.show()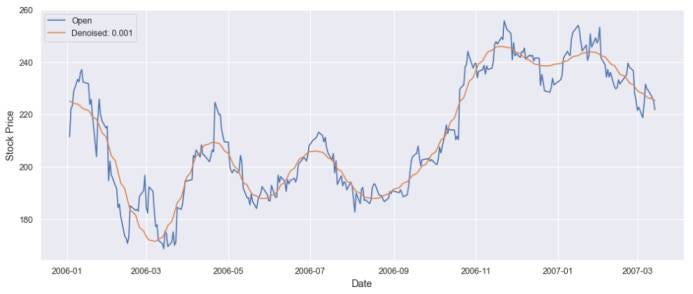

Outlier Detection in Time Series

An outlier in time series refers to a sudden peak or drop in the trend line. We are not concerned with the factors causing the outliers, but certainly, there can be multiple factors. We will keep ourselves confined with the detection of outliers. Let’s take a look at the available methods for detecting the outliers:

• Rolling Statistical Bound based approach

This method is most intuitive and works for almost all kinds of time series. In this method, upper and lower bounds are created based on specific statistical measures like mean and standard deviation, Z and T scores, and percentile of the distributions. For instance, we can define our upper and lower bound as:

Taking the mean and standard deviation of the whole series is not advisable for outlier detection since the bound would be static in that case. The bounds should be created on a rolling basis, like considering a continuous set of observations to create bounds and then shifting to another window. This method is highly effective and simple for outlier detection. 

• Isolation Forest

As the name suggests, Isolation forest is a decision tree-based machine learning algorithm for anomaly detection. It works by isolating the data points on a given set of features using the decision tree’s partitions. In other words, It takes a sample out of the dataset and builds trees over that sample until each point is isolated. To isolate a data point, partitions are made randomly by selecting a split between the max and min values of that feature until each point is isolated. Random partition of features will create shorter paths in trees for the anomalous data points and thus distinguishing them from the rest of the data.

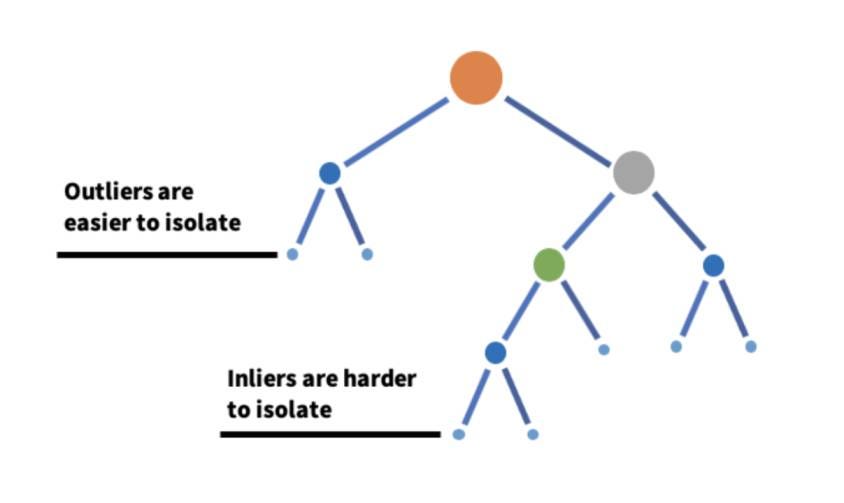
Source: Medium

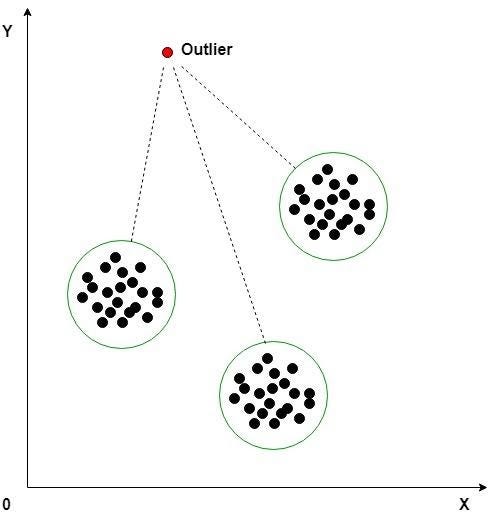
• K-means Clustering

K-means clustering is again an unsupervised machine learning algorithm frequently used to detect outliers in time series data. This algorithm looks at the data point in the dataset and groups the similar data points into K number of clusters. Anomalies are distinguished by measuring the distance of a data point to its nearest centroid. If the distance is greater than a certain threshold value, the data point is marked as an anomaly. K-Means algorithm uses the Euclidean Distances for comparison. 

Possible Interview Questions

If one is writing a project on time-series in their CV, then the interviewer can ask these possible questions from this topic:

1. What are the ways to preprocess the time-series data, and how is it different from standard imputation methods?
2. What does it mean by a time-series window?
3. Have you heard of the Isolation forest method? If yes, then can you explain how does it work?
4. What is Fourier transform, and why do we need that?
5. What are the different methods to correct the missing values in time-series data?

Conclusion 

In this tutorial, we looked at some common time series data preprocessing techniques. We started with ordering the time-series observations; then, we looked at various missing value imputation techniques. We found that the time-series imputations are different from the conventional imputation techniques since we deal with an ordered set of observations. Further, we applied some noise removal techniques to the google stock price dataset and finally discussed some outlier detection methods for time series. Using all these mentioned preprocessing steps ensures high-quality data, ready for building complex models. 

Enjoy Learning! Enjoy Pre-processing! Enjoy Algorithms!