Rain Water Trapping Problem
Difficulty: Hard, Asked-in: Google, Microsoft, Amazon.
Key takeaway: An excellent problem to learn time and space complexity optimization using various approaches. Two-pointers and stack-based approaches are worth exploring.
Let’s understand the problem
Given n non-negative integers representing an elevation map where the width of each tower is 1. Write a program to compute how much water it can trap after raining.
Example
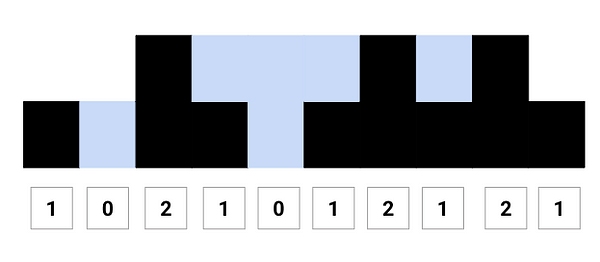
Input: height[] = [1, 0, 2, 1, 0, 1, 2, 1, 2, 1], Output: 6
Explanation: Trapped water = 1 x 1 + 1 x 1 + 2 x 1 + 1 x 1 + 1 x 1 = 6 (Area of the blue region in the following diagram).
Discussed solution approaches
- Brute force solution using nested loops
- Using single loop and extra memory
- Using stack data structure
- Efficient approach using two pointers
Brute force solution using nested loops
Solution idea
One basic idea would be to traverse the array, calculate the rainwater trapped at each tower, and sum it to get the overall water trapped. The critical question is: How do we find the amount of water trapped at each tower?
If we observe closely, water trapped by tower height[i] will be bounded by the minimum of the maximum height on the left and right sides of height[i]. So here is the formula: Rainwater trapped at height[i] = min (max height on the left side, max height on the right side) - height[i].
So for each element height[i], we traverse elements on the left of height[i] to find the highest tower on the left side and traverse elements on the right of height[i] to find the highest tower on the right side. After this, we apply the above formula to calculate the water trapped at tower height[i].
Solution steps
- We initialize the variable trappedWater to store the total trapped water.
-
Now, we traverse the array from i = 0 to n - 1. Inside the loop, we initialize variables leftMax and rightMax to track the maximum height of towers on both sides. For each height[i]:
- We run a loop from j = i to 0 to find the maximum height on the left side and store this value in the variable leftMax. Similarly, we run a loop from j = i to n - 1 to find the maximum height on the right side and store this value in the variable rightMax.
- Using the formula, we calculate the amount of water trapped at height[i] and add it to the variable trappedWater: trappedWater = trappedWater + min(leftMax, rightMax) - height[i].
- By the end of nested loops, we return value stored in variable trappedWater.
Solution code C++
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
int trappedWater = 0;
for (int i = 0; i < n; i = i + 1)
{
int leftMax = 0;
for (int j = i; j >= 0; j = j - 1)
leftMax = max(height[j], leftMax);
int rightMax = 0;
for (int j = i; j < n; j = j + 1)
rightMax = max(height[j], rightMax);
trappedWater = trappedWater + min(leftMax, rightMax) - height[i];
}
return trappedWater;
}Solution code Python
def rainWaterTrapping(height, n):
if n < 3:
return 0
trapped_water = 0
for i in range(n):
left_max = 0
for j in range(i, -1, -1):
left_max = max(height[j], left_max)
right_max = 0
for j in range(i, n):
right_max = max(height[j], right_max)
trapped_water = trapped_water + min(left_max, right_max) - height[i]
return trapped_waterSolution analysis
We use two nested loops where the outer loop scans the height[] array, and the two inner loops find rightMax and leftMax. So, at each iteration of the outer loop, we traverse each array element using the inner loops. Therefore, the time complexity is n * O(n) = O(n^2). We use a constant number of variables, so the space complexity is O(1).
Using single loop and extra memory
Solution idea
Now critical questions are: Can we improve efficiency and solve the problem in O(n) time? Is it possible to get rid of the two inner loops? Let's think! If we know the values of leftMax and rightMax for each tower height[i], we can solve this problem in a single scan of the array. How can we do this? Let's think!
Suppose we take two extra arrays, leftMax[n] and rightMax[n], i.e., leftMax[i] to store the maximum height on the left side and rightMax[i] to store the maximum height on the right side. Can we calculate both arrays in O(n) time? Here is an idea:
- If we know leftMax[i - 1], we can easily calculate leftMax[i] in O(1) using the formula leftMax[i] = max(leftMax[i - 1], height[i]).
- Similarly, if we know rightMax[i + 1], we can easily calculate rightMax[i] in O(1) using the formula rightMax[i] = max(rightMax[i + 1], height[i]).
So, based on the above idea, we can store values in the leftMax[] and rightMax[] arrays in a single scan of the height[] array. This is similar to the dynamic programming approach where we use the already calculated solution of the smaller problem to get the solution to the larger problem. Think!
Solution steps
- We create two arrays leftMax[n] and rightMax[n].
- Now we initialize leftMax[0] with height[0] and run a loop from i = 1 to n - 1 to store values in leftMax[]. At each ith iteration, we store the maximum element that occurred up to that point in leftMax[i].
- Similarly, we initialize rightMax[n - 1] with height[n - 1] and run a loop from i = n - 2 to 0 to store values in rightMax[]. At each ith iteration, we store the maximum element that occurred up to that point in rightMax[i].
- Now stored water at the height[i] = min(leftMax[i], rightMax[i]) - height[i]. So we traverse the height[] array and track the total amount of trapped water using the variable trappedWater.
- Finally, we return the value stored in the variable trappedWater.
Solution code C++
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
int leftMax[n], rightMax[n];
leftMax[0] = height[0];
for (int i = 1; i < n; i = i + 1)
leftMax[i] = max(leftMax[i - 1], height[i]);
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; i = i - 1)
rightMax[i] = max(rightMax[i + 1], height[i]);
int trappedWater = 0;
for (int i = 0; i < n; i = i + 1)
trappedWater = trappedWater + min(leftMax[i], rightMax[i]) - height[i];
return trappedWater;
}Solution code Python
def rainWaterTrapping(height, n):
if n < 3:
return 0
left_max = [0] * n
right_max = [0] * n
left_max[0] = height[0]
for i in range(1, n):
left_max[i] = max(left_max[i - 1], height[i])
right_max[n - 1] = height[n - 1]
for i in range(n - 2, -1, -1):
right_max[i] = max(right_max[i + 1], height[i])
trapped_water = 0
for i in range(n):
trapped_water = trapped_water + min(left_max[i], right_max[i]) - height[i]
return trapped_waterSolution analysis
We are running three single loops. So, the time complexity = Time complexity of storing values in leftMax[] + Time complexity of storing values in rightMax[] + Time complexity of calculating total trapped water = O(n) + O(n) + O(n) = O(n). We are using two extra arrays of size n. So the space complexity = Space complexity of leftMax[] + Space complexity of rightMax[] = O(n) + O(n) = O(n).
Using stack data structure
Solution idea
The critical question is: Can we solve this problem in a single scan of height[] array? Let's explore.
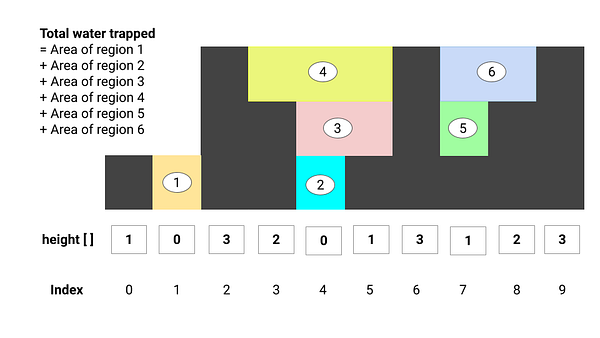
- Region 1 Area = Area bounded between index 2 and 0
- Region 2 Area = Area bounded between index 5 and 3
- Region 3 Area = Area bounded between index 6 and 3
- Region 4 Area = Area bounded between index 6 and 2
- Region 5 Area = Area bounded between index 8 and 6
- Region 6 Area = Area bounded between index 9 and 6
Did we observe any patterns? Here's an idea: As we traverse the array, we need to find the area confined between the current tower and all previous smaller towers in a sequence. The critical question is: How can we find this? One idea would be to use a stack to track the indices of the previous smaller towers.
We will keep pushing towers onto the stack until we find a tower larger than the one at the top of the stack. Now We'll stop at this stage because there can be some trapped water on the left side of the current tower. So we get the indices of the previous smaller towers by popping values from the stack and calculate the amount of water stored at each popped tower and the current tower.
Solution steps
Step 1: We create a stack, S, to store indices of previous smaller towers. Now, we traverse the height[] array using a loop while(i < n).
Step 2: If the current tower is smaller than or equal to the tower at the top of the stack, we push the index of the current tower onto the stack and move to the next tower.
Step 3: If the current tower height[i] is larger than the tower at the top of the stack, we can conclude that there may be trapped water between the current tower and some previous towers in the stack. So, we pop the value from the stack, calculate the trapped water, and add it to the total trapped water. The water trapped is equal to the area of the rectangular region formed by the current tower, the popped tower, and the tower at the top of the stack.
- Region width = Current index - Index of the top stack element - 1.
- Region height = min(Height of the current tower, Height of the tower at the top of the stack) - Height of the popped tower.
- Water trapped = Region width x Region height.
We continue this step in a loop until we find the current tower smaller than the tower at the top of the stack or the stack becomes empty.
Step 4: Finally, we return the value stored in the variable trappedWater.
Solution code C++
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
int trappedWater = 0;
int i = 0;
stack<int> S;
while (i < n)
{
while (!S.empty() && height[i] > height[S.top()])
{
int topTower = S.top();
S.pop();
if (S.empty())
break;
int regionWidth = i - S.top() - 1;
int regionHeight = min(height[i], height[S.top()]) - height[topTower];
trappedWater = trappedWater + regionWidth * regionHeight;
}
S.push(i);
i = i + 1;
}
return trappedWater;
}Solution code Python
def rainWaterTrapping(height, n):
if n < 3:
return 0
trappedWater = 0
i = 0
S = []
while i < n:
while S and height[i] > height[S[-1]]:
topTower = S.pop()
if not S:
break
regionLength = i - S[-1] - 1
regionHeight = min(height[i], height[S[-1]]) - height[topTower]
trappedWater = trappedWater + regionLength * regionHeight
S.append(i)
i = i + 1
return trappedWaterSolution code Java
class RainWater
{
public int rainWaterTrapping(int[] height, int n)
{
if (n < 3)
return 0;
int trappedWater = 0;
int i = 0;
Stack<Integer> S = new Stack<>();
while (i < n)
{
while (!S.empty() && height[i] > height[S.peek()])
{
int topTower = S.pop();
if (S.empty())
break;
int regionLength = i - S.peek() - 1;
int regionHeight = Math.min(height[i], height[S.peek()]) - height[topTower];
trappedWater = trappedWater + regionLength * regionHeight;
}
S.push(i);
i = i + 1;
}
return trappedWater;
}
}Solution analysis
We are performing a single traversal of the array. In the worst case, we will perform two stack operations for each tower, i.e., one push and one pop operation. So the time complexity = O(n). In the worst case, the stack can contain up to n elements, so the space complexity is O(n).
Efficient solution using two pointers approach
Solution idea and steps
Here is an observation: For a given tower, if there is any tower on the right side that is taller than the maximum height on the left side, the amount of water trapped at the current tower will depend on the maximum height on the left side. Vice versa is also true: If there is any tower on the left side taller than the maximum height on the right side, the amount of water trapped at the current tower will depend on the maximum height on the right side.
So one idea is to traverse the array from the opposite end using two pointers (l and r) and maintain two extra variables (maxLeft and maxRight) to track the maximum heights encountered from both ends. Initial values: l = 0, r = n - 1, leftMax = 0, rightMax = 0. This will continue in a loop until the left pointer does not cross the right pointer i.e. while (l <= r).
If height[l] < height[r]: If there are some towers on the left side shorter than height[r], there can be some trapped water at these left towers. So we calculate the water trapped at towers on the left side, update maxLeft, keep moving the left pointer forward and stop the left pointer when height[l] is greater than height[r]. During this process:
- If height[l] < maxLeft, there will be some water at height[l]. The water trapped at height[l] is equal to maxLeft - height[l].
- If height[l] > maxLeft, then we find a new maximum height from the left, and there will be no water at height[l]. So we update maxLeft with the value of height[l].
if (height[l] < height[r])
{
if (height[l] > leftMax)
leftMax = height[l]
else
trappedWater = trappedWater + leftMax - height[l]
l = l + 1
}If height[l] > height[r]: There will be some towers on the right side shorter than height[l], and there can be trapped water at these right towers. We continue a similar process: calculate the trapped water at towers on the right side, update maxRight, move the right pointer inward and stop the right pointer when height[r] is greater than height[l]. During this process:
- If height[r] < maxRight, there will be some water at height[r]. The water trapped at height[r] is equal to maxRight - height[r].
- If height[r] > maxRight, then we find a new maximum height from the right, and there will be no water at height[r]. So we update maxRight with the value of height[r].
if (height[l] > height[r])
{
if (height[r] > rightMax)
rightMax = height[r]
else
trappedWater = trappedWater + rightMax - height[r]
r = r - 1
}In simple terms: If the shorter tower is on the left end, the amount of trapped water will depend on the tower's height in the direction from left to right. Similarly, if the shorter tower is on the right end, the amount of trapped water will depend on the tower's height in the direction from right to left.
So we first calculate the water trapped on the shorter tower among height[l] and height[r] and move the pointer associated with the shorter tower. In terms of an analogy, we can think of height[l] and height[r] as forming a partial container wall, where we fix the higher end and allow water to flow from the lower end.
Solution code C++
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
int trappedWater = 0;
int leftMax = 0, rightMax = 0;
int l = 0, r = n - 1;
while (l <= r)
{
if (height[l] < height[r])
{
if (height[l] > leftMax)
leftMax = height[l];
else
trappedWater = trappedWater + leftMax - height[l];
l = l + 1;
}
else
{
if (height[r] > rightMax)
rightMax = height[r];
else
trappedWater = trappedWater + rightMax - height[r];
r = r - 1;
}
}
return trappedWater;
}Solution code Python
def rainWaterTrapping(height, n):
if n < 3:
return 0
trappedWater = 0
leftMax = 0
rightMax = 0
l = 0
r = n - 1
while l <= r:
if height[l] < height[r]:
if height[l] > leftMax:
leftMax = height[l]
else:
trappedWater = trappedWater + leftMax - height[l]
l = l + 1
else:
if height[r] > rightMax:
rightMax = height[r]
else:
trappedWater = trappedWater + rightMax - height[r]
r = r - 1
return trappedWaterSolution analysis
We are doing a single scan to traverse the array from both ends. After each comparison, we move either the left or right pointer. So in the worst case, we need to do O(n) operations. So, time complexity = O(n).
Only constant space is required for variables and pointers, so space complexity = O(1).
Critical ideas to think!
Can we find another solution to this problem in O(n) time and O(1) space? Here is a hint: we first search for the maximal tower in height [] and split the array into two halves around it. Now we do two traversals: One from the leftmost tower to the highest tower and another from the rightmost to the highest tower.
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
int maxIndex = 0; // Index of the maximum tower.
int trappedWater = 0;
// Find the maximum tower's index.
for (int i = 0; i < n; i = i + 1)
{
if (height[i] > height[maxIndex])
maxIndex = i;
}
int leftMax = height[0];
for (int i = 1; i < maxIndex; i = i + 1)
{
if (height[i] < leftMax)
trappedWater = trappedWater + leftMax - height[i];
else
leftMax = height[i];
}
int rightMax = height[n - 1];
for (int i = n - 2; i > maxIndex; i = i - 1)
{
if (height[i] < rightMax)
trappedWater = trappedWater + rightMax - height[i];
else
rightMax = height[i];
}
return trappedWater;
}In the 2nd approach, can we save one extra array? Here is a hint: We pre-calculate the max height on the left side of each tower in an array maxLeft[i]. Now we process the trapped water on the fly as we traverse the towers from right to left. During this process, we maintain a variable maxRight to keep track of the maximum height on the right side. For each tower, we calculate the min(maxLeft[i], maxRight). If this minimum is greater than the height[i], it means there's trapped water at height[i]. After that, we update maxRight.
int rainWaterTrapping(int height[], int n)
{
if (n < 3)
return 0;
// Maximum height on the left side of each tower.
int maxLeft[n];
// Maximum height on the right side.
int maxRight = 0;
int trappedWater = 0;
// Calculate maximum height on the left side of each tower.
for (int i = 1; i < n; i = i + 1)
maxLeft[i] = max(maxLeft[i - 1], height[i - 1]);
for (int i = n - 2; i >= 0; i = i - 1)
{
int minMax = min(maxLeft[i], maxRight);
// Calculate trapped water for the current tower.
if (minMax > height[i])
trappedWater = trappedWater + minMax - height[i];
// Update maximum height on the right side.
maxRight = max(maxRight, height[i]);
}
return trappedWater;
}- In the stack-based approach, what would be the best and worst-case scenarios?
- In the 4th approach, can we compare leftMax and rightMax to decide which pointer to move?
- Let's consider a different version of the problem: given an m x n integer matrix height[][] representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after rain.
Comparisons of time and space complexities
- Brute force approach: Time = O(n²), Space = O(1).
- Using dynamic programming: Time = O(n), Space = O(n).
- Using stack: Time = O(n), Space = O(n).
- Using two pointers: Time = O(n), Space = O(1).
Similar coding questions to practice
- Container with most water
- Check for pair in an array with a given sum
- Sort an array of 0s, 1s, and 2s
- Remove duplicates from sorted array
- Equilibrium index of an array
Please write comments if you find an error or you want to share more insights about the topic. Enjoy learning, Enjoy coding, Enjoy algorithms!
Share Your Insights
More from EnjoyAlgorithms
Self-paced Courses and Blogs
Coding Interview
OOP Concepts
Our Newsletter
Subscribe to get well designed content on data structure and algorithms, machine learning, system design, object orientd programming and math.
©2023 Code Algorithms Pvt. Ltd.
All rights reserved.
