Container With Most Water

Difficulty: Medium, Asked-in: Google, Facebook, Amazon, Adobe

Key takeaway: An excellent coding problem to learn problem-solving using the two-pointers approach, where both pointers are moving in the opposite direction. The idea and proof behind the efficient solution are intuitive and worth exploring. 

Let’s understand the problem

Given an array of n non-negative integers height [n], where each value represents a point at coordinate (i, height[i]). Now n vertical lines are drawn such that the two endpoints of line i are at (i, 0) and (i, height[i]). Here each pair of a line with the x-axis forms a container.

Write a program to find two lines, such that the container contains the most water. We should return an integer that corresponds to the maximum area of water that can be contained.

Problem note

• The value of n is at least 2.
• We need to maximize the area formed between the vertical lines using the shorter line as height and the distance between the lines as the width i.e Area = max [(j  -  i) * min (height[i], height[j])].

Important note: before moving on to the solutions, we recommend trying this problem on paper for atleast 15 or 30 minutes. Enjoy problem-solving!

Example

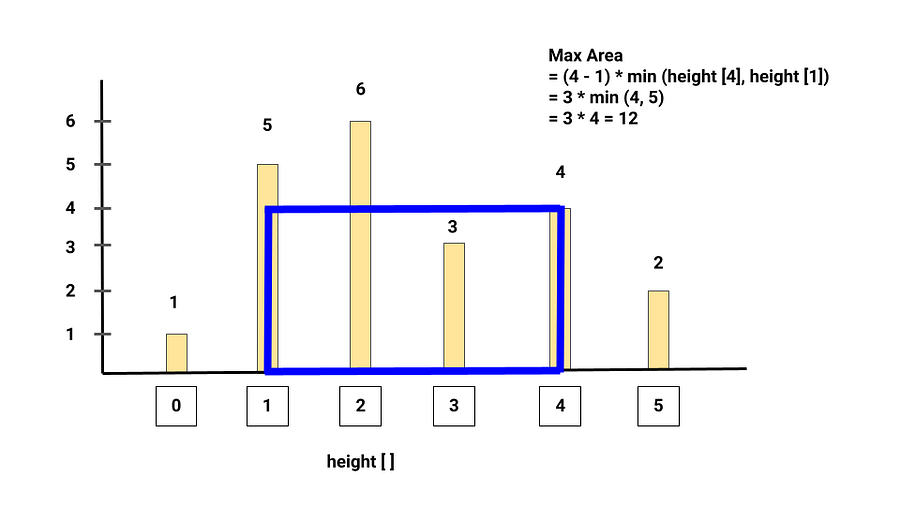
Input: height[] = [1, 5, 6, 3, 4, 2], Output: 12

Explanation: The area between lines 5 and 4 will be maximum. 5 and 4 are distance 3 apart, so the size of the base = 3. Height of container = min(5, 4) = 4, So total area = 3 * 4 = 12. Refer to the following image for better clarity.

Discussed solution approaches

• Brute force approach  using nested loops
• Efficient solution  using two pointers

Brute force approach  using nested loops

Solution idea and steps

The basic idea would be to consider every possible pair of lines and find the maximum area out of those pairs. Area between each pair of lines(i, j) = (j - i) * min (height[j], height[i]) (Think!)

• We initialize a variable maxArea to track the max area between pairs of lines.
• We run a nested loop to consider each pair of lines: the outer loop from i = 0 to n - 1 and the inner loop from j = i to n - 1.
• We calculate the area using the above formula for every pair of lines i and j and store it in a temporary variable currArea. If currArea > maxArea, we update the maxArea i.e maxArea = max (maxArea, currArea)
• By the end of the nested loops, we return the value stored in the variable maxArea.

Solution code C++

int maxContainerWater(int height[], int n) 
{
    int maxArea = 0;
    for (int i = 0; i < n; i = i + 1) 
    {
        for (int j = i; j < n; j = j + 1) 
        {
            int currArea = (j - i) * min(height[i], height[j]);
            maxArea = max(maxArea, currArea);
        }
    }
    return maxArea;
}

Solution code Python

def max_container_water(height, n):
    max_area = 0
    for i in range(n):
        for j in range(i, n):
            curr_area = (j - i) * min(height[i], height[j])
            max_area = max(max_area, curr_area)
    return max_area

Solution analysis

We are considering every possible pair of lines using two nested loops. Total no. of pairs = n(n-1)/2 (Think!). Time complexity = O(n²). Space complexity = O(1), we are using a constant number of variables.

Efficient solution  using two pointers approach

Solution idea

Now the critical questions are: how can we improve the time complexity? What kind of information do we use to optimize it further? In the above approach, we are exploring all the pairs of i and j calculating the area using the formula (j - i) * min (height[j], height[i]). So rather than choosing all pairs, can we cover all possibilities of (i, j) in a wise way and do it using a single loop? Think!

Here is a solution idea: we take two pointers, one at the beginning and one at the end of the height[] array, and maintain a variable maxArea to store the maximum area between the lines. At every step, we calculate the area formed between the two pointers, update the maxArea and move the pointer pointing to the shorter line towards the other end by one. But a critical question is: why are we doing this? Here is an explanation by considering two possible scenarios when (height[i] < height[j]) and (height[i] > height[j]).

Case 1: if (height[i] < height[j])

When height[i] < height[j], we don’t need to calculate the area for all pairs between (i, j - 1), (i, j - 2),…because these areas are smaller than the area at (i, j). Let's understand it better by comparing the area for (i, j) and (i, j - 1).

• A = Area for pair (i, j) = (j  - i) * min (height[i], height[j]) = (j  -  i) * height[i]
• A’ = Area for pair (i, j - 1) = (j  - 1  -  i) * min (height[i], height[j - 1])

if(height[i] < height[j - 1])

=> A’ = (j  -  1  -  i) * min (height[i], height[j - 1]) = (j - 1 - i) * height[i]

=> A' = (j - 1 - i) * height[i] < (j - i) * height[i] (As we know, A = (j - i) * height[i])

=> A’ < A

if(height[i] > height[j - 1])

=> A’ = (j  -  1  -  i) * min (height[i], height[j - 1]) = (j - 1 - i) * height[j-1]

=> A’ = (j - 1 - i) * height[j-1] < (j - i) * height[i] (As we know, A = (j - i) * height[i])

=> A' < A

So overall, when height[i] < height[j], the area between pair of lines (i, j) is less than (i, j - 1). With a similar argument, areas between the pairs (i, j - 2), (i, j - 3),…will be automatically less than the area between the pair (i, j). In simple words: we don’t need to consider the area between the pairs (i, j - 1), (i, j - 2), (i, j - 3), etc., and move the pointer i to one right in search of a larger area. Think!

Case 2: if (height[i] > height[j])

When height[i] > height[j], we don’t need to calculate all (i + 1, j), (i + 2, j),…because these areas are smaller than our area at (i, j). So we move the pointer j to one left in search of a larger area. We can use an idea similar to the above approach for the proof. (Think!)

Solution steps

• We initialize the variable maxArea to store the maximum area.
• We use two pointers i and j initialized at 0 and n-1, respectively. 
• Now we run a loop till the left pointer i is less than the right pointer j.
• We calculate the area formed between pointers i and j using the formula (j - i)*min(height[i], height[j]) and update the maxArea.
• if (height[i] < height[j]), we move pointer i by one right. Otherwise, we move pointer j by one left.
• By the end of the loop, our max area gets stored in the variable maxArea.

Solution code C++

int maxContainerWater(int height[], int n)
{
    int maxArea = 0;
    int i = 0;
    int j = n - 1;
    while (i < j)
    {
        int currArea = (j - i) * min(height[i], height[j]);
        maxArea = max(maxArea, currArea);
        if (height[i] < height[j])
            i = i + 1;
        else
            j = j - 1;
    }
    return maxArea;
}

Solution code Python

def max_container_water(height, n):
    max_area = 0
    i = 0
    j = n - 1
    while i < j:
        curr_area = (j - i) * min(height[i], height[j])
        max_area = max(max_area, curr_area)
        if height[i] < height[j]:
            i = i + 1
        else:
            j = j - 1
    return max_area

Solution analysis

At every iteration of the while loop, we perform one comparison and move one pointer by 1. In the worst case, we are scanning the input array once using the left and right pointers. Time complexity = O(n)(Think!). Space complexity = O(1), we are using a constant number of variables.

Critical ideas to think!

• Can we solve this problem using another approach?
• For the area for the pair (i, j), why do we require a minimum of height[i] and height[j]?
• Does the above solution work when values are repeated i.e. any two vertical lines have the same height? In this scenario, how do we modify the above code to get the correct output? How do we decide to move pointers? 
• Visualize the correctness of the two-pointer approach.

Comparisons of time and space complexities

• Using nested loops : Time = O(n^2), Space = O(1)
• Using two pointers: Time = O(n), Space = O(1)

Similar coding questions to practice

• Trapping rain-water
• Triplet with zero-sum
• Check for pair in an array with a given sum
• The intersection of two sorted array
• Whether an array is a subset of another array
• Merge two sorted arrays of the same size
• Find the maximum j – i such that A[j] > A[i]
• Count the number of possible triangles
• Find four elements that sum to a given value

Enjoy learning, Enjoy coding, Enjoy algorithms!