Divide and Conquer vs Dynamic Programming

Divide and conquer and dynamic programming are popular problem-solving approaches in data structures and algorithms. Both approaches share a similarity: they break problems into smaller subproblems and combine their solutions to solve the larger problem. But there are significant differences between divide and conquer and dynamic programming in several aspects:

• The nature of the subproblems involved in the solution
• The thought process in building recursive solutions
• Analysis of time and space complexity
• Types of problems they solve

Let's explore these differences in detail.

Differences based on the nature of the sub-problems

In the divide and conquer approach, problems get divided into independent subproblems, which are solved separately to get the final solution. On the other hand, in dynamic programming, problems get divided into dependent subproblems, which are solved in a specific order to get the final solution.

In the context of algorithms, independent means that the solution to one subproblem does not affect the solution to another subproblem. So, subproblems can be solved separately. An example of this is the idea of merge sort, where we divide the input array into two equal subarrays. Then, we recursively sort these two subproblems, treating each subarray as a separate problem.

On the other hand, dependent means that the solution to one subproblem relies on the solution to one or more smaller subproblems. So, the subproblems must be solved in a specific order.

An example of this is the problem of finding the nth Fibonacci. For finding the nth Fibonacci, we use the solutions of the two subproblems: Finding the (n - 1)th and (n - 2)th Fibonacci. To calculate the (n - 1)th Fibonacci, we use the solution to the (n - 2)th and (n - 3)th Fibonacci. In other words, here subproblems are dependent because we can not solve nth Fibonacci and (n - 1)th Fibonacci until we find the solution of (n-2)th Fibonacci.

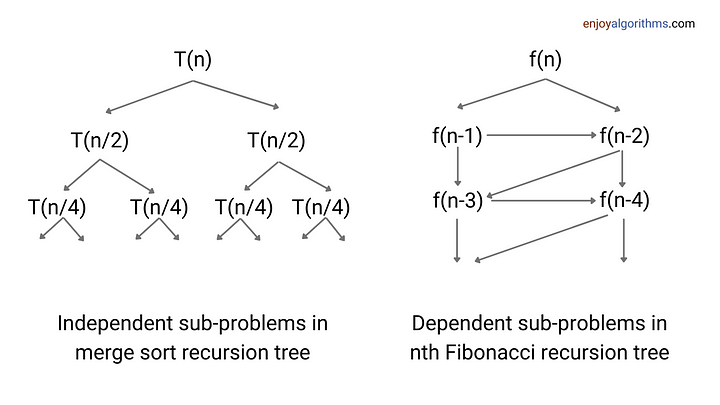
When subproblems are dependent during recursion, it will create unnecessary recursive calls. This is due to one reason: the algorithm repeatedly solves the same subproblems. To solve this issue, we use dynamic programming, where we solve each subproblem only once and store the solution in an array or lookup table. This will avoid redundant calculations of the same subproblem and improve the time complexity.

Differences in terms of thought process of recursive solutions

In the divide and conquer approach, we divide the problem into two or more equally sized subproblems. Then, we solve each subproblem recursively and combine their solutions to get the final solution. Here the problem is recursively divided into smaller subproblems until a base case is reached, where the subproblems are simple enough to be solved directly.

In the recursive solution of a dynamic programming problem, our goal is to explore all possibilities recursively to get the final solution. So solution space is very large and due to this, the time complexity of the recursive solution becomes exponential. That's why we use top-down and bottom-up approaches in dynamic programming to solve such problems efficiently.

Although the recursive solution to DP problems is inefficient, it guides us in implementing both the top-down and bottom-up approaches.

• The top-down approach is similar to the recursive solution, where we use extra memory to store solutions to sub-problems. Here we start from larger problems and move top-down to smaller subproblems.
• The bottom-up approach is an iterative approach, which is just the reverse idea of the top-down approach. Here, we start from smaller subproblems and move to larger problems, storing their solutions in additional memory. You can explore this blog: Top-down vs Bottom-up Approach of dynamic programming.

Dynamic programming can be slightly more challenging than divide and conquer because figuring out how to build a recursive solution can be difficult. The key idea is to identify the initial choices available in the problem and based on those choices, decompose the problem into smaller subproblems. With practice, one can master this idea easily.

Differences in terms of analysis techniques

Time complexity analysis

We can analyze divide and conquer algorithms using either the recursion tree method or the master theorem. The master theorem is a simple technique for analyzing divide and conquer algorithms. In the recursion tree method, we define a recurrence relation, calculate the total number of operations performed at each level, and then sum them up level by level.

On the other hand, the recursive solution for dynamic programming problems often involves a complex recurrence relation, which makes it unsuitable for applying the master theorem. In such cases, we can use the recursion tree method or apply basic combinatorial ideas for analysis.

• When we implement dynamic programming using the recursive top-down approach (memoization), we explore all different subproblems and perform some additional operations to solve each subproblem. If the time complexity of the additional operation is O(1), the overall time complexity = O(count of different subproblems) * O(1) = O(count of different subproblems).
• When we implement dynamic programming using the bottom-up approach (tabulation), we analyze the algorithm by counting the number of loop iterations and multiplying it by the time complexity of each iteration. In each iteration, we mostly solve one subproblem in O(1) time complexity. So, the overall time complexity = O(count of different subproblems) * O(1) = O(count of different subproblems).

Space complexity analysis

In the divide-and-conquer approach, the space complexity primarily depends on the size of the recursive call stack, which is equal to the maximum depth of the recursion tree. Sometimes, we also use extra space to combine the solutions to the subproblems. A good example of this is the merge sort algorithm, which uses O(n) extra space.

In dynamic programming, we typically use O(1), O(n), or O(n^2) additional memory to store the solutions of the subproblems. This is the idea of time memory tradeoff, where we use extra memory to reduce the time complexity from exponential time to polynomial time.

• The top-down approach is recursive, so recursion will use a call stack. The space complexity of the top-down approach = O(size of the call stack) + O(extra space to store subproblem solutions). In most cases, the extra space required for storing subproblem solutions will dominate the space complexity.
• The bottom-up approach is iterative and it doesn't have the overhead of a recursion call stack. So space complexity of the bottom-up approach is equal to the extra space to store subproblem solutions.

Input size of the subproblems

In a divide-and-conquer, the input size of the subproblems decreases quickly by a factor of some constant at each recursive call. Due to this, the height of the recursion tree will be O(log n). The best examples are merge sort and binary search, where the input size decreases by a factor of 1/2 (e.g. n -> n/2 -> n/4 and so on).

In dynamic programming, the input size of the subproblems decreases slowly by some constant during recursive calls. So the height of the recursion tree will be a linear function of the input size, such as O(n). Because of this, the stack space used in the recursive implementation of dynamic programming problems is larger compared to the stack space used in divide-and-conquer problems.

Differences in terms of problems they solve

Dynamic programming is mostly used to solve optimization problems, where the goal is to find the best solution among many possible solutions. It is also used for counting problems, where the objective is to count the number of ways or arrangements that satisfy certain conditions. You can explore this blog: Types of problems solved using dynamic programming.

On the other hand, divide and conquer is not limited to a specific problem type or solution space size. It can be used in various scenarios, such as sorting, searching, and even optimization problems.

We hope you enjoyed the blog. If you have any queries or feedback, please write us at contact@enjoyalgorithms.com. Enjoy learning, Enjoy algorithms!